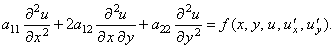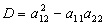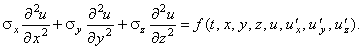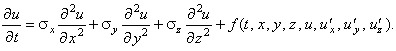Дифференциальные уравнения в частных производных 2-го порядка не имеют единого метода численного решения. Поэтому следует рассмотреть их классификацию, позволяющую использовать единые методы для численного решения каждого из подтипов этих уравнений.
     Общий вид дифференциального уравнения 2-го порядка в частных производных при условии, что искомая функция зависит от двух переменных, можно представить следующим образом: В зависимости от знака величины

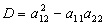(1.1)

дифференциальные уравнения в частных производных 2-го порядка относят к уравнениям:

при D > 0 - гиперболического типа, при D < 0 - эллиптического типа, при D = 0 - параболического типа.

     Принадлежность многомерных дифференциальных уравнений в частных производных 2-го порядка к тому или иному типу определяют, руководствуясь следующими правилами.
     1. Если в уравнении присутствуют производные 2-го порядка по всем независимым переменным и знаки перед ними одинаковые - то данное уравнение относят к уравнениям эллиптического типа, например:      2. Если в уравнении отсутствует производная 2-го порядка хотя бы по одной из независимых переменных - то данное уравнение относят к уравнениям параболического типа, например: