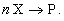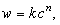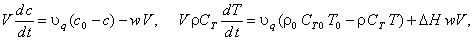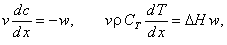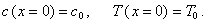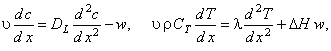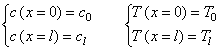|
Рассмотрим примеры математических моделей химических реакторов, в которых протекает простая необратимая реакция типа
Скорость такой реакции определяется по формуле:
где k - константа скорости химической реакции; с - концентрация вещества Х.
1. Математическая модель проточного реактора идеального смешения включает балансы по концентрации
компонента Х и температуре:
где 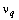 - объёмный расход поступающего раствора; - объёмный расход поступающего раствора;
 H - тепловой эффект реакции;
V - рабочий объём реактора; H - тепловой эффект реакции;
V - рабочий объём реактора;
 - теплоёмкость, плотность и температура смеси в реакторе;
индекс (0) означает значение параметра на входе в реактор. - теплоёмкость, плотность и температура смеси в реакторе;
индекс (0) означает значение параметра на входе в реактор.
Таким образом, математическая модель состоит из двух обыкновенных
дифференциальных уравнений 1-го порядка, которые необходимо дополнить начальными условиями (задача Коши):
2. Математическая модель трубчатого реактора (идеального вытеснения)
в стационарном режиме имеет вид:
где v - линейная скорость потока; х - координата по длине реактора.
Данная математическая модель также состоит из двух обыкновенных
дифференциальных уравнений 1-го порядка, которые необходимо дополнить граничными условиями:
3. Математическая модель трубчатого реактора с продольным перемешиванием в стационарном режиме имеет вид:
где DL ,  - коэффициенты диффузии и теплопроводности. - коэффициенты диффузии и теплопроводности.
Данная математическая модель состоит из двух обыкновенных дифференциальных
уравнений 2-го порядка, которые необходимо дополнить граничными условиями:
Здесь l - длина реактора.
|
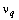 - объёмный расход поступающего раствора;
- объёмный расход поступающего раствора;
 H - тепловой эффект реакции;
V - рабочий объём реактора;
H - тепловой эффект реакции;
V - рабочий объём реактора;
 - теплоёмкость, плотность и температура смеси в реакторе;
индекс (0) означает значение параметра на входе в реактор.
- теплоёмкость, плотность и температура смеси в реакторе;
индекс (0) означает значение параметра на входе в реактор.
 - коэффициенты диффузии и теплопроводности.
- коэффициенты диффузии и теплопроводности.