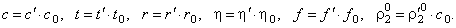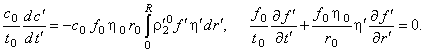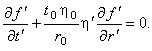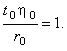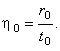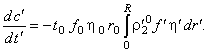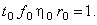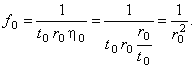|
1.2. Методика определения неизвестных характерных параметров процесса
Рассмотрим методику определения неизвестных характерных параметров.
Для этого выразим переменные математической модели через характерные и безразмерные значения:
Затем подставим их в исходную систему уравнений (2.1):
| |
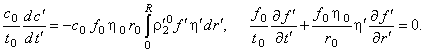 |
(2.2) |
Рассмотрим второе уравнение в системе (2.2), которое после
несложных преобразований можно представить в виде:
Для того чтобы полученное обезразмеренное уравнение совпало с исходным, комплекс характерных
параметров, стоящий перед вторым слагаемым, необходимо приравнять единице:
Следовательно, характерное значение скорости роста кристаллов определяется по формуле:
| |
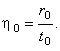 |
(2.3) |
Рассмотрим теперь первое уравнение в системе (2.2), которое
после несложных преобразований можно привести к виду:
Для того чтобы полученное обезразмеренное уравнение совпало с исходным, комплекс характерных
параметров, стоящий перед интегралом в правой части уравнения, необходимо приравнять единице:
Отсюда, используя соотношение (2.3), получаем характерное значение плотности функции распределения
кристаллов по размерам:
| |
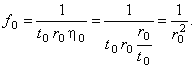 |
(2.4) |
Таким образом, если характерные значения скорости роста
кристаллов и плотности функции распределения кристаллов по размерам соответствуют выражениям (2.3),
(2.4), то оба уравнения в системе (2.2) полностью совпадают с исходными уравнениями математической
модели процесса кристаллизации (2.1). Однако порядки переменных в уравнениях системы (2.1)
различны (например, функция f имеет порядок 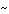 1020, а 1020, а 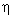 - - 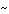 10-10), вследствие чего расчётные ошибки при
определении функции f , не значимые для неё самой, могут привести к сильным искажениям значений 10-10), вследствие чего расчётные ошибки при
определении функции f , не значимые для неё самой, могут привести к сильным искажениям значений 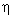 .
В то же время при численном решении уравнений системы (2.2) этого не произойдёт, так как все
переменные в них имеют одинаковый порядок. .
В то же время при численном решении уравнений системы (2.2) этого не произойдёт, так как все
переменные в них имеют одинаковый порядок.
|
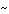 1020, а
1020, а 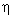 -
- 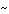 10-10), вследствие чего расчётные ошибки при
определении функции f , не значимые для неё самой, могут привести к сильным искажениям значений
10-10), вследствие чего расчётные ошибки при
определении функции f , не значимые для неё самой, могут привести к сильным искажениям значений 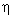 .
В то же время при численном решении уравнений системы (2.2) этого не произойдёт, так как все
переменные в них имеют одинаковый порядок.
.
В то же время при численном решении уравнений системы (2.2) этого не произойдёт, так как все
переменные в них имеют одинаковый порядок.