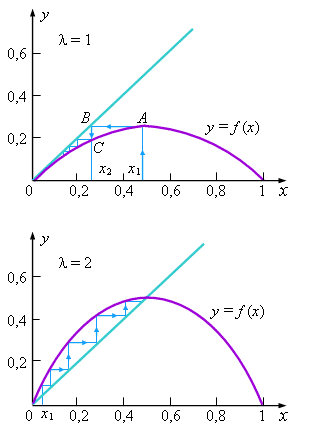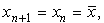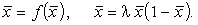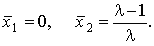1. Бифуркация удвоения периода
|
1.2. Неподвижные точки одномерного отображения
Изучим динамику популяции, т.е. вид последовательности
При небольших 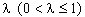 значение
значение 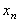 стремится к нулю независимо
от выбора стремится к нулю независимо
от выбора 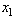 ,
т. е. популяция, численность которой мы рассматриваем, выжить не может, сколько бы бактерий не было вначале.
Поведение последовательности удобно представить графически. Построим кривую ,
т. е. популяция, численность которой мы рассматриваем, выжить не может, сколько бы бактерий не было вначале.
Поведение последовательности удобно представить графически. Построим кривую 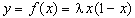 при одном из рассматриваемых значений
при одном из рассматриваемых значений  и прямую у = х (см. рисунок). Отложим
и прямую у = х (см. рисунок). Отложим 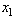 по оси абсцисс, проведём вертикаль до пересечения с кривой у = f (x) (точка А),
затем горизонталь до пересечения с прямой у = х (точка В) и снова вертикаль до пересечения
с кривой y = f (x) (точка С с координатой
по оси абсцисс, проведём вертикаль до пересечения с кривой у = f (x) (точка А),
затем горизонталь до пересечения с прямой у = х (точка В) и снова вертикаль до пересечения
с кривой y = f (x) (точка С с координатой 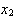 ).
Легко проверить, что ).
Легко проверить, что 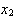 = f ( = f (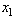 ).
Взяв точку ).
Взяв точку 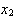 за начальную и повторив
те же операции, получим за начальную и повторив
те же операции, получим 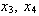 и т. д.
Из рисунка видно, что и т. д.
Из рисунка видно, что 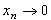 при при 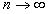 . .
Из формулы (14.2) следует, что функция f (x) переводит отрезок [0, 1] в отрезок [0, 1/4]. Если 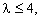 то все значения то все значения 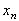 лежат на отрезке [0, 1] при условии, что
лежат на отрезке [0, 1] при условии, что 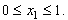 Именно поэтому говорят, что формула (14.2) задаёт отображение отрезка на себя.
Именно поэтому говорят, что формула (14.2) задаёт отображение отрезка на себя.
При значениях  ,
немного больших 1, последовательность ,
немного больших 1, последовательность 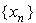 стремится к некоторому постоянному значению
стремится к некоторому постоянному значению 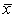 ,
зависящему от ,
зависящему от  . Следовательно,
численность популяции с течением времени стабилизируется (см. рисунок). Для модели (14.2)
это означает, что, начиная с некоторого момента, будет выполняться равенство: . Следовательно,
численность популяции с течением времени стабилизируется (см. рисунок). Для модели (14.2)
это означает, что, начиная с некоторого момента, будет выполняться равенство:
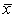 из уравнения: из уравнения:
 < 1 квадратное уравнение (14.3)
имеет один неотрицательный корень < 1 квадратное уравнение (14.3)
имеет один неотрицательный корень 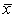 = 0.
При = 0.
При  > 1 квадратное уравнение (14.3) имеет два неотрицательных корня: > 1 квадратное уравнение (14.3) имеет два неотрицательных корня:
 = 1 происходит бифуркация:
в системе появляется устойчивая неподвижная точка = 1 происходит бифуркация:
в системе появляется устойчивая неподвижная точка 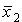 ,
а точка ,
а точка 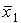 теряет устойчивость. теряет устойчивость.
|
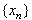 при
при 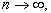 при различных значениях параметра
при различных значениях параметра