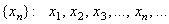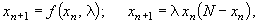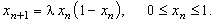|
1.1. Дискретная модель для описания популяции бактерий
До сих пор мы рассматривали упорядоченное движение.
При наличии в системе неподвижной точки центр возникают периодические колебания,
если неподвижная точка - устойчивый фокус, то - затухающие колебания.
В системе, имеющей предельный цикл, также возникают периодические колебания.
Если же система обладает странным аттрактором, то движение теряет свою периодичность и
возникают непериодические колебания. В этом разделе на примере простой дискретной системы мы
рассмотрим один из возможных сценариев перехода от упорядоченного движения к хаосу через каскад бифуркаций
типа удвоения периода, один из возможных механизмов возникновения хаотического множества в фазовом пространстве.
Рассмотрим процесс роста бактерий в биореакторе (ферментёре).
Если один раз за характерный период времени определять количество бактерий (х), мы получим последовательность,
описывающую изменение численности бактерий:
Естественно ожидать, что численность популяции в данный момент времени зависит от того, сколько бактерий было в
ферментёре в момент предыдущего замера. Математическая модель изменения численности популяции часто
представляется в виде:
| |
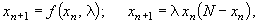 |
(14.1) |
где  - коэффициент роста численности популяции; N - максимальное значение численности вида. - коэффициент роста численности популяции; N - максимальное значение численности вида.
Из уравнения (14.1) видно, что численность популяции быстро растёт,
пока она мала 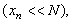 и начинает убывать, когда бактерий становится слишком много. и начинает убывать, когда бактерий становится слишком много.
Если провести обезразмеривание модели (14.1) с помощью соотношений
тогда она примет следующий вид (штрихи опущены):
Уравнения типа (14.2) называются логистическими.
|
 - коэффициент роста численности популяции; N - максимальное значение численности вида.
- коэффициент роста численности популяции; N - максимальное значение численности вида.
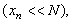 и начинает убывать, когда бактерий становится слишком много.
и начинает убывать, когда бактерий становится слишком много.