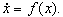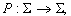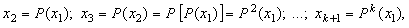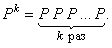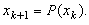|
2.3. Отображение Пуанкаре
Кроме принципа подчинения переменных существует ещё
один механизм исследования периодического движения с понижением порядка системы - метод сечений Пуанкаре.
Пусть 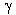 - замкнутая траектория системы - замкнутая траектория системы
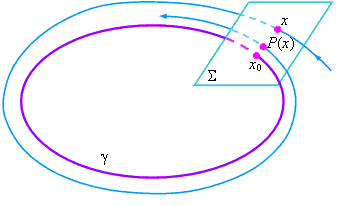
Выберем на этой траектории точку х0 и проведём через неё сечение 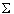 ,
представляющее собой малую часть плоскости, которая трансверсально (под ненулевым углом)
пересекает траекторию ,
представляющее собой малую часть плоскости, которая трансверсально (под ненулевым углом)
пересекает траекторию 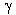 в точке х0 (см. рисунок). в точке х0 (см. рисунок).
Траектории системы (15.4), близкие к замкнутой траектории, задают отображение Р
сечения 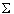 на себя следующим образом.
Возьмём на сечении Пуанкаре на себя следующим образом.
Возьмём на сечении Пуанкаре 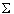 точку х,
через которую проходит траектория точку х,
через которую проходит траектория 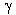 (х).
Обозначим Р(х) первую точку пересечения траектории (х).
Обозначим Р(х) первую точку пересечения траектории 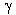 (х)
с сечением (х)
с сечением 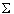 , которая следует после х. Тем самым мы определим отображение
называемое отображением Пуанкаре, как замкнутую траекторию , которая следует после х. Тем самым мы определим отображение
называемое отображением Пуанкаре, как замкнутую траекторию 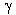 . .
Метод исследования систем с помощью сечения Пуанкаре заключается в изучении
последовательности точек 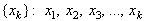 пересечения
поверхности Пуанкаре с траекториями. Последовательность пересечения
поверхности Пуанкаре с траекториями. Последовательность 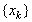 определяется с помощью отображения P следующим образом:
где символом P k(x) обозначается k-я итерация отображения Р:
Заметим, что в таком представлении динамика системы выглядит как некоторое
рекуррентное соотношение с дискретным временем, поскольку интервалы времени между последовательными
пересечениями поверхности
определяется с помощью отображения P следующим образом:
где символом P k(x) обозначается k-я итерация отображения Р:
Заметим, что в таком представлении динамика системы выглядит как некоторое
рекуррентное соотношение с дискретным временем, поскольку интервалы времени между последовательными
пересечениями поверхности 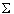 траекторией конечны: траекторией конечны:
|
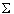 ,
представляющее собой малую часть плоскости, которая трансверсально (под ненулевым углом)
пересекает траекторию
,
представляющее собой малую часть плоскости, которая трансверсально (под ненулевым углом)
пересекает траекторию 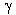 в точке х0 (см. рисунок).
в точке х0 (см. рисунок).
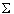 на себя следующим образом.
Возьмём на сечении Пуанкаре
на себя следующим образом.
Возьмём на сечении Пуанкаре 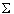 точку х,
через которую проходит траектория
точку х,
через которую проходит траектория 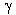 (х).
Обозначим Р(х) первую точку пересечения траектории
(х).
Обозначим Р(х) первую точку пересечения траектории 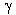 (х)
с сечением
(х)
с сечением 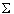 , которая следует после х. Тем самым мы определим отображение
, которая следует после х. Тем самым мы определим отображение
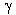 .
.
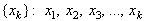 пересечения
поверхности Пуанкаре с траекториями. Последовательность
пересечения
поверхности Пуанкаре с траекториями. Последовательность 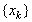 определяется с помощью отображения P следующим образом:
определяется с помощью отображения P следующим образом:
 траекторией конечны:
траекторией конечны: