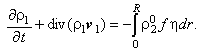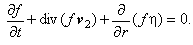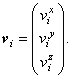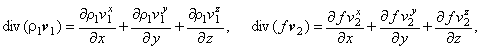|
Уравнение сохранения массы для сплошной фазы имеет вид:
| |
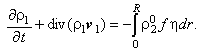 |
(2.1) |
Закон сохранения массы для дисперсной фазы отражает уравнение баланса
числа включений с учётом изменения объёма включения за счёт фазового перехода:
| |
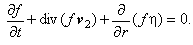 |
(2.2) |
Отметим, что уравнение (2.2) записано для r-фазы. Для получения уравнения
сохранения массы всей дисперсной фазы надо умножить каждый член уравнения (2.2) на 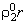 и проинтегрировать его по dr
от 0 до R.
и проинтегрировать его по dr
от 0 до R.
При написании уравнений (2.1) и (2.2) использованы следующие обозначения:
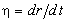 - наблюдаемая скорость изменения размера
(объёма) включения; R - наибольший размер включений; - наблюдаемая скорость изменения размера
(объёма) включения; R - наибольший размер включений;
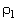 - средняя плотность сплошной фазы; - средняя плотность сплошной фазы;
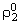 - истинная плотность дисперсной фазы; - истинная плотность дисперсной фазы;
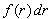 - число включений в единице объёма смеси с размером от r до r + dr; - число включений в единице объёма смеси с размером от r до r + dr;
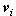 - вектор средней массовой скорости i-й фазы (здесь и далее векторные величины в формулах выделяются полужирным шрифтом):
Вторые члены в левых частях уравнений (2.1) и (2.2) учитывают движение смеси.
Дивергенцию можно представить более подробно:
где - вектор средней массовой скорости i-й фазы (здесь и далее векторные величины в формулах выделяются полужирным шрифтом):
Вторые члены в левых частях уравнений (2.1) и (2.2) учитывают движение смеси.
Дивергенцию можно представить более подробно:
где 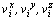 - проекции вектора средней массовой скорости i-й фазы на оси координат. - проекции вектора средней массовой скорости i-й фазы на оси координат.
Член в правой части уравнения (2.1) и третий член в левой части уравнения (2.2)
отражают суммарное влияние фазового перехода на включениях.
|
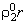 и проинтегрировать его по dr
от 0 до R.
и проинтегрировать его по dr
от 0 до R.
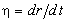 - наблюдаемая скорость изменения размера
(объёма) включения; R - наибольший размер включений;
- наблюдаемая скорость изменения размера
(объёма) включения; R - наибольший размер включений;
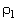 - средняя плотность сплошной фазы;
- средняя плотность сплошной фазы;
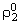 - истинная плотность дисперсной фазы;
- истинная плотность дисперсной фазы;
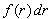 - число включений в единице объёма смеси с размером от r до r + dr;
- число включений в единице объёма смеси с размером от r до r + dr;
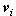 - вектор средней массовой скорости i-й фазы (здесь и далее векторные величины в формулах выделяются полужирным шрифтом):
- вектор средней массовой скорости i-й фазы (здесь и далее векторные величины в формулах выделяются полужирным шрифтом):
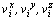 - проекции вектора средней массовой скорости i-й фазы на оси координат.
- проекции вектора средней массовой скорости i-й фазы на оси координат.