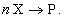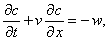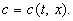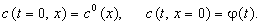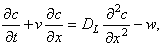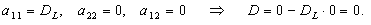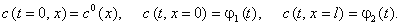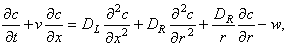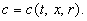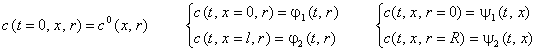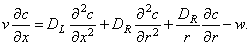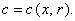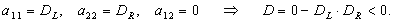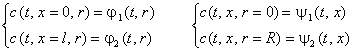Рассмотрим еще несколько примеров математических моделей химических реакторов, в которых протекает простая необратимая реакция типа
     4. Математическая модель (баланс по концентрации компонента Х) трубчатого реактора в нестационарном режиме имеет вид: причём концентрация компонента Х является функцией двух переменных: Данное уравнение необходимо дополнить начальным и граничным условиями:
     5. Математическая модель трубчатого реактора с продольным перемешиванием в нестационарном режиме имеет вид: причём концентрация компонента Х является функцией двух переменных:      Определим тип данного уравнения с помощью выражения (1.1): Следовательно, данное уравнение является уравнением параболического типа. Его необходимо дополнить начальным и двумя граничными условиями:
     6. Математическая модель трубчатого реактора с продольным и поперечным перемешиванием в нестационарном режиме имеет вид: где r - координата по радиусу реактора; D_L , D_R - коэффициенты диффузии в продольном и поперечном направлениях.
     Данное уравнение является многомерным, поскольку концентрация компонента Х - функция трёх переменных: Так как отсутствует производная 2-го порядка по времени, данное уравнение является уравнением параболического типа. Его необходимо дополнить начальным и граничными условиями: Здесь R - радиус реактора.

     7. Математическая модель трубчатого реактора с продольным и поперечным перемешиванием в стационарном режиме имеет вид: Концентрация компонента Х в данном случае - функция двух переменных:      Определим тип данного уравнения с помощью выражения (1.1): Следовательно, данное уравнение является уравнением эллиптического типа. Его необходимо дополнить граничными условиями: