Используя введённые обозначения, запишем аппроксимацию дифференциальных операторов, составляющих уравнение (7.1), в точке 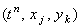. Для аппроксимации производной функции u по времени обычно используется правая конечная разность (со стабилизацией значения независимой переменной х в точке с порядковым номером j, а значения независимой переменной y в точке с порядковым номером k): Для аппроксимации второй производной функции u по координате х будем использовать разностный оператор (2.12) (со стабилизацией значения независимой переменной y в точке с порядковым номером k, а значения независимой переменной t в точке с порядковым номером n): Для аппроксимации второй производной функции u по координате y также будем использовать разностный оператор (2.12) (со стабилизацией значения независимой переменной х в точке с порядковым номером j, а значения независимой переменной t в точке с порядковым номером n):      Подставляя записанные разностные операторы в дифференциальное уравнение (7.1), получаем явную разностную схему, аппроксимирующую уравнение (7.1) в точке :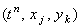

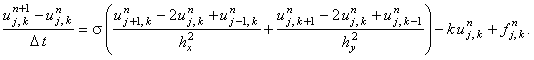(7.2)

     Рассматривая аппроксимацию обеих производных второго порядка на (n + 1)-ом шаге по времени, получаем неявную разностную схему:

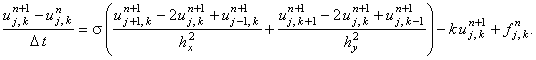(7.3)

     Учитывая порядок аппроксимации разностных операторов, использованных при составлении разностных схем (7.2), (7.3), легко видеть, что они имеют первый порядок аппроксимации по времени и второй - по каждой из координат:
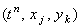
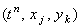