2. Система Лоренца
|
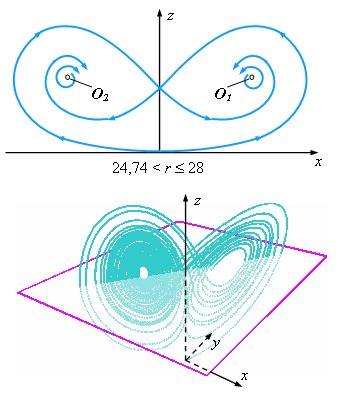
2.4. Фазовый портрет аттрактора Лоренца
Рассмотрим поведение системы (13.1) при
При 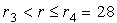 все стационарные точки (O, O1 и O2)
являются неустойчивыми. Единственным устойчивым предельным множеством - аттрактором - будет B2,
т. е. аттрактор Лоренца (см. рисунок). Следовательно, в системе (13.1)
при любых начальных условиях будет устанавливаться хаотический режим движения. Хаотическая траектория аттрактора,
представленного на рисунке (внизу), просчитывалась при
все стационарные точки (O, O1 и O2)
являются неустойчивыми. Единственным устойчивым предельным множеством - аттрактором - будет B2,
т. е. аттрактор Лоренца (см. рисунок). Следовательно, в системе (13.1)
при любых начальных условиях будет устанавливаться хаотический режим движения. Хаотическая траектория аттрактора,
представленного на рисунке (внизу), просчитывалась при 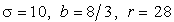 и начальных условиях
и начальных условиях 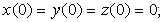 плоскость (x, y) соответствует z = 27. плоскость (x, y) соответствует z = 27.
Таким образом, можно сделать вывод, что диссипативные динамические системы (например, система Лоренца), размерность фазового пространства которых больше или равна трём, могут иметь наряду с регулярными и очень сложные, хаотические режимы движения. Математическим представлением такого хаотического поведения диссипативных систем является притягивающее множество сложной структуры - странный аттрактор. |
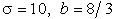 и
и 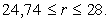
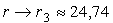 седловые предельные циклы L1 и L2
стягиваются соответственно к стационарным точкам O1 и O2
и при r = r3 исчезают, сливаясь с ними; согласно
седловые предельные циклы L1 и L2
стягиваются соответственно к стационарным точкам O1 и O2
и при r = r3 исчезают, сливаясь с ними; согласно