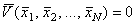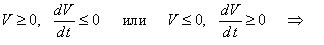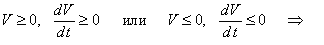|
Под устойчивостью стационарного состояния физико-химической системы понимают её
невосприимчивость к случайным флуктуациям, то есть случайным кратковременным изменениям значений управляющих
параметров системы (концентраций компонентов, температуры окружающей среды, скорости протока реагентов через
реактор и т.п.). Если стационарное состояние системы является устойчивым, то случайные флуктуации не будут
оказывать существенного воздействия на поведение системы. Если же стационарное состояние неустойчиво, тогда под
воздействием случайных флуктуаций система самопроизвольно перейдёт в качественно новое состояние.
Для исследования устойчивости систем существует два метода, разработанных
русским математиком А.М. Ляпуновым. Первый метод Ляпунова основан на определении корней характеристического
уравнения системы дифференциальных уравнений, описывающей физико-химическую систему (подробно он будет рассмотрен
во второй части курса в разделе "Методы исследования линейных систем"). Второй метод Ляпунова основан на
исследовании физико-химической системы с помощью функции Ляпунова.
Определение. Рассмотрим некоторое стационарное состояние системы 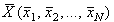 .
Если найдётся функция .
Если найдётся функция 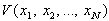 , которая равна нулю в стационарном состоянии , которая равна нулю в стационарном состоянии
| |
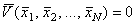 |
|
и знакоопределена в его окрестности, т.е.
| |
 |
|
то такую функцию называют функцией Ляпунова.
Второй метод Ляпунова заключается в исследовании знака производной от функции
Ляпунова dV/dt. Если в окрестности рассматриваемого стационарного состояния знак функции Ляпунова V отличается
от знака её производной dV/dt, то такое стационарное состояние устойчиво; если же знаки функции Ляпунова V и её
производной dV/dt совпадают, то стационарное состояние неустойчиво:
| |
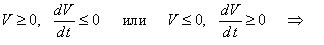 |
состояние устойчиво; |
| |
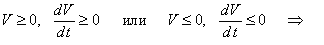 |
состояние неустойчиво. |
|
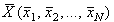 .
Если найдётся функция
.
Если найдётся функция 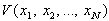 , которая равна нулю в стационарном состоянии
, которая равна нулю в стационарном состоянии