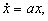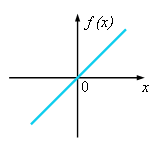4. Классификация неподвижных точек на прямой
|
4.2. Репеллер
Дифференциальное уравнение
 > 0 динамику цепной реакции, имеет единственную неподвижную точку  .
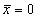На рисунке представлен фазовый портрет дифференциального уравнения (7.12), а также график функции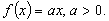 
Функция 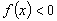 слева от неподвижной точки
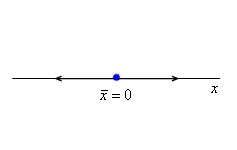
и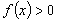 
справа от неё. Следовательно, траектории расходятся от неподвижной точки.
В рассмотренном примере неподвижная точка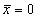
- неустойчивая. Такой тип неподвижной точки на прямой, когда траектории расходятся от неё с обеих сторон, называется репеллером.
|
