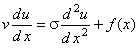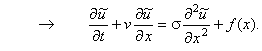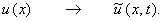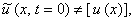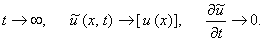|
Представим стационарную задачу, описываемую уравнением (10.1)
для случая k = 0 (т.е., когда метод прогонки неприменим),
в нестационарном виде. Для этого в уравнение (10.1) необходимо добавить фиктивную производную по времени:
| |
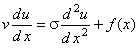 |
(10.3) |
| |
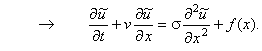 |
(10.4) |
При этом искомая функция станет уже функцией двух переменных:
Полученное уравнение (10.4) относится к одномерным дифференциальным уравнениям параболического типа,
методы численного решения которых мы уже рассматривали. Таким образом, возникает вопрос: можно ли для
решения уравнения (10.3) воспользоваться решением уравнения (10.4)? Чтобы получить ответ на этот вопрос,
следует проанализировать результат численного решения уравнения (10.4).
Известно, что численное решение нестационарной задачи (10.4)
требует задания начального условия. Если оно будет отличаться от истинного решения стационарной задачи (10.3):
то производная по времени не будет равна нулю и в ходе численного решения уравнения (10.4) возникнет
некоторая динамика, т.е. изменение значений 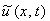 при при 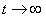 . .
Однако поскольку в качестве граничных условий для численного решения нестационарной задачи (10.4)
используются граничные условия исходной стационарной задачи
т.е. граничные условия, не зависящие от времени, то с течением времени (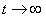 )
производная по времени будет стремиться к нулю, а решение )
производная по времени будет стремиться к нулю, а решение 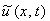 нестационарной задачи (10.4) - к решению стационарной задачи (10.3): нестационарной задачи (10.4) - к решению стационарной задачи (10.3):
| |
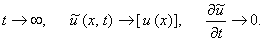 |
(10.5) |
Таким образом, использование граничных условий, не зависящих от времени, даёт положительный ответ на поставленный вопрос.
Данный метод решения стационарной задачи путём преобразования её в
нестационарную получил название метода установления. Процесс пошагового приближения решения
нестационарной задачи к решению исходной стационарной задачи называют итерационным процессом,
переход от n-го шага к (n + 1)-му - итерацией, значение 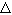 t - шагом итерации,
а индекс п - номером итерации. t - шагом итерации,
а индекс п - номером итерации.
|
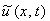 при
при 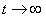 .
.
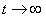 )
производная по времени будет стремиться к нулю, а решение
)
производная по времени будет стремиться к нулю, а решение 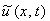 нестационарной задачи (10.4) - к решению стационарной задачи (10.3):
нестационарной задачи (10.4) - к решению стационарной задачи (10.3):
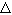 t - шагом итерации,
а индекс п - номером итерации.
t - шагом итерации,
а индекс п - номером итерации.