Запишем обыкновенное дифференциальное уравнение второго порядка в следующем общем виде:

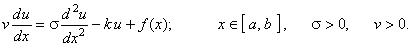(10.1)

Уравнение (10.1) следует дополнить граничными условиями (для определённости будем рассматривать граничные условия 1-го рода):      Запишем для уравнения (10.1) разностную схему, аппроксимируя производную второго порядка разностным оператором (2.12), а производную первого порядка - левой конечной разностью (в соответствии с правилом выбора конечных разностей для аппроксимации первых производных по координатам):

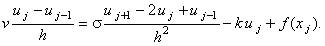(10.2)

Отметим, что в случае v < 0 для аппроксимации производной первого порядка следует использовать правую конечную разность.
     Приведём разностную схему (10.2) к виду (4.10), удобному для использования метода прогонки: Следовательно, коэффициенты, соответствующие уравнению (4.10), имеют вид: Проверяя для разностной схемы (10.2) достаточное условие сходимости прогонки (4.16) приходим к выводу, что оно выполняется только при условии k > 0. Алгоритм решения (в виде блок-схемы) разностной схемы (10.2) для этого случая представлен на рисунке.      При k = 0 достаточное условие сходимости прогонки (4.16) не выполняется и, следовательно, для решения разностной схемы (10.2) в этом случае метод прогонки использовать нельзя.