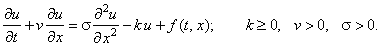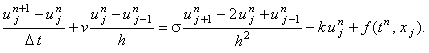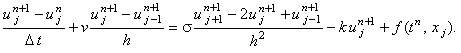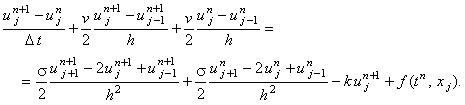6. Сравнительная характеристика изученных разностных схем.
|
В заключение приведём сравнительную характеристику разностных схем, аппроксимирующих одномерное дифференциальное уравнение параболического типа, содержащее производную по координате первого порядка:
1. Явная разностная схема
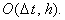 Условно устойчива
Условно устойчива 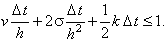 Решается с помощью рекуррентного соотношения (6.4).
Решается с помощью рекуррентного соотношения (6.4).
2. Неявная разностная схема
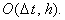 Абсолютно устойчива.
Решается методом прогонки.
Абсолютно устойчива.
Решается методом прогонки.
3. Разностная схема Кранка-Николсона
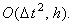 Абсолютно устойчива.
Решается методом прогонки.
Абсолютно устойчива.
Решается методом прогонки.
Напомним, что в случае v < 0 для аппроксимации
производной по координате первого порядка следует использовать правую конечную разность.
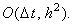 Абсолютно устойчива.
Решается методом прогонки, сходящейся при выполнении одного из условий: (6.9) или (6.10).
Абсолютно устойчива.
Решается методом прогонки, сходящейся при выполнении одного из условий: (6.9) или (6.10).
|