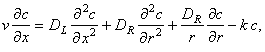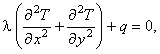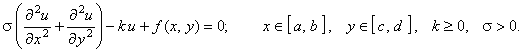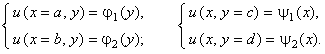1. Примеры дифференциальных уравнений эллиптического типа.
|
В разделе "Примеры математических моделей, содержащих дифференциальные уравнения в частных производных" мы рассматривали математическую модель трубчатого реактора с продольным и поперечным перемешиванием, в котором протекает простая необратимая реакция. Баланс по концентрации исходного реагента для стационарного режима имеет вид:
Данное уравнение является дифференциальным уравнением эллиптического типа. Другим примером дифференциального уравнения эллиптического типа является уравнение теплопроводности для стационарного двумерного температурного поля:
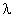 - теплопроводность материала;
x, y - пространственные координаты; q - внутренний источник (сток) теплоты. - теплопроводность материала;
x, y - пространственные координаты; q - внутренний источник (сток) теплоты.
Для простоты дальнейшего изложения представим дифференциальное уравнение эллиптического типа в следующем общем виде:
|