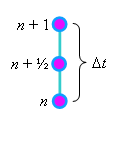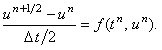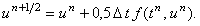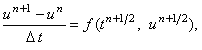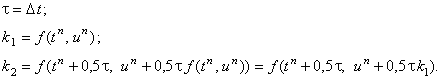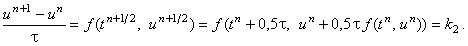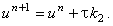|
Рассмотрим метод решения уравнения (12.1), имеющий второй порядок точности.
Для этого разобьём пополам интервал 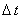 между точками между точками
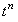 и и 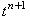 (см. рисунок).
Полученную промежуточную точку обозначим, как (см. рисунок).
Полученную промежуточную точку обозначим, как 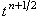 . Запишем явную разностную схему,
аппроксимирующую уравнение (12.1) на первом полушаге интервала . Запишем явную разностную схему,
аппроксимирующую уравнение (12.1) на первом полушаге интервала 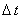 (т.е., на интервале
(т.е., на интервале 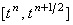 ):
Следовательно, решение в точке ):
Следовательно, решение в точке 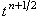 можно найти с помощью рекуррентного соотношения: можно найти с помощью рекуррентного соотношения:
| |
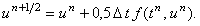 |
(12.5) |
Зная решение в точке 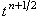 ,
можно записать для уравнения (12.1) разностную схему, в которой производная по времени будет
аппроксимирована центральной конечной разностью: ,
можно записать для уравнения (12.1) разностную схему, в которой производная по времени будет
аппроксимирована центральной конечной разностью:
| |
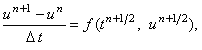 |
(12.6) |
где 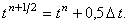 Видно, что правая часть разностной схемы (12.6)
аппроксимируется относительно точки Видно, что правая часть разностной схемы (12.6)
аппроксимируется относительно точки 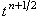 . Следовательно, разностный оператор в левой части является
центральной конечной разностью, которая, как известно, имеет второй порядок аппроксимации. . Следовательно, разностный оператор в левой части является
центральной конечной разностью, которая, как известно, имеет второй порядок аппроксимации.
Введём следующие обозначения:
| |
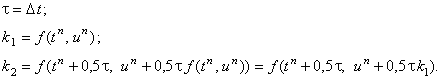 |
(12.7) |
С учётом рекуррентного соотношения (12.5) и обозначений (12.7) разностная схема (12.6) будет иметь вид:
Таким образом, решение на (n + 1)-ом шаге по времени можно найти с помощью рекуррентного соотношения:
Описанный метод решения обыкновенных дифференциальных уравнений первого порядка носит название
метода Рунге-Кутта 2-го порядка.
|
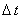 между точками
между точками
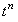 и
и 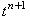 (см. рисунок).
Полученную промежуточную точку обозначим, как
(см. рисунок).
Полученную промежуточную точку обозначим, как 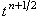 . Запишем явную разностную схему,
аппроксимирующую уравнение (12.1) на первом полушаге интервала
. Запишем явную разностную схему,
аппроксимирующую уравнение (12.1) на первом полушаге интервала 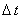 (т.е., на интервале
(т.е., на интервале 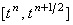 ):
):
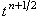 можно найти с помощью рекуррентного соотношения:
можно найти с помощью рекуррентного соотношения:
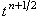 ,
можно записать для уравнения (12.1) разностную схему, в которой производная по времени будет
аппроксимирована центральной конечной разностью:
,
можно записать для уравнения (12.1) разностную схему, в которой производная по времени будет
аппроксимирована центральной конечной разностью:
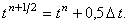 Видно, что правая часть разностной схемы (12.6)
аппроксимируется относительно точки
Видно, что правая часть разностной схемы (12.6)
аппроксимируется относительно точки 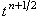 . Следовательно, разностный оператор в левой части является
центральной конечной разностью, которая, как известно, имеет второй порядок аппроксимации.
. Следовательно, разностный оператор в левой части является
центральной конечной разностью, которая, как известно, имеет второй порядок аппроксимации.