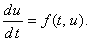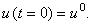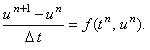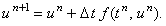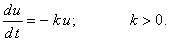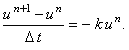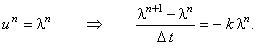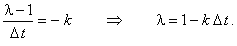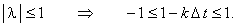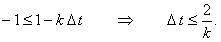|
Запишем обыкновенное дифференциальное уравнение первого порядка в следующем общем виде:
| |
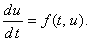 |
(12.1) |
Уравнение (12.1) следует дополнить начальным условием:
Запишем для уравнения (12.1) явную разностную схему:
| |
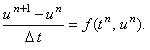 |
(12.2) |
Метод решения обыкновенных дифференциальных уравнений первого порядка с использованием явной
разностной схемы (12.2) называется явным методом Эйлера.
Разностная схема (12.2) имеет первый порядок аппроксимации по времени. Для её решения используется
рекуррентное соотношение:
Для анализа устойчивости явного метода Эйлера рассмотрим конкретный пример:
| |
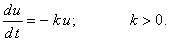 |
(12.3) |
Явная разностная схема для уравнения (12.3) имеет вид:
Проведём исследование устойчивости данной схемы с помощью спектрального метода:
Упрощаем данное выражение, деля левую и правую его части на 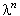 ,
и выражаем ,
и выражаем  :
С учётом необходимого условия устойчивости разностных схем (3.8) имеем:
В полученном двойном неравенстве правое условие выполняется автоматически.
Поэтому рассмотрим более подробно левое условие:
Полученное выражение является условием устойчивости явной разностной схемы, аппроксимирующей уравнение (12.3). :
С учётом необходимого условия устойчивости разностных схем (3.8) имеем:
В полученном двойном неравенстве правое условие выполняется автоматически.
Поэтому рассмотрим более подробно левое условие:
Полученное выражение является условием устойчивости явной разностной схемы, аппроксимирующей уравнение (12.3).
Таким образом, явный метод Эйлера является условно устойчивым и относится к методам с первым порядком точности.
|
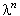 ,
и выражаем
,
и выражаем  :
: