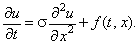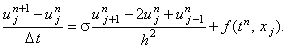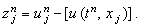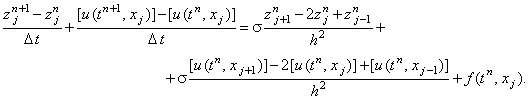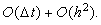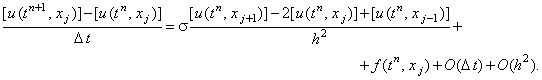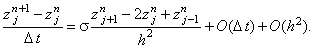|
В настоящем учебном пособии изучается два метода,
позволяющих исследовать устойчивость разностных схем. Первый из них называется
гармоническим или спектральным методом анализа разностных схем. Второй - метод тестовых
задач - будет описан в конце курса.
Рассмотрим одномерное дифференциальное уравнение
параболического типа, свободный член которого не включает искомую функцию u:
| |
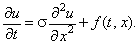 |
(3.3) |
Запишем для него явную разностную схему:
| |
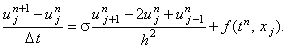 |
(3.4) |
Погрешность решения разностной схемы (3.4)
в точке 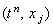 можно представить с помощью соотношения:
Здесь можно представить с помощью соотношения:
Здесь 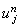 - решение разностной схемы (3.4)
в точке - решение разностной схемы (3.4)
в точке 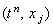 ; ;
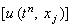 - истинное решение исходного дифференциального уравнения (3.3)
в точке - истинное решение исходного дифференциального уравнения (3.3)
в точке 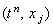 . Выражая из данного соотношения . Выражая из данного соотношения 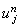 и подставляя в разностную схему (3.4), получаем:
и подставляя в разностную схему (3.4), получаем:
В разделе "Порядок аппроксимации разностной схемы"
было доказано, что разностная схема (3.4) имеет порядок аппроксимации:
Следовательно, имеет место следующее равенство:
С учётом данного выражения получаем разностную схему для погрешности решения:
| |
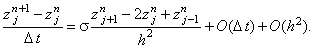 |
(3.5) |
|
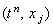 можно представить с помощью соотношения:
можно представить с помощью соотношения:
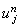 - решение разностной схемы (3.4)
в точке
- решение разностной схемы (3.4)
в точке 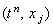 ;
;
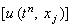 - истинное решение исходного дифференциального уравнения (3.3)
в точке
- истинное решение исходного дифференциального уравнения (3.3)
в точке 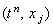 . Выражая из данного соотношения
. Выражая из данного соотношения 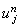 и подставляя в разностную схему (3.4), получаем:
и подставляя в разностную схему (3.4), получаем: