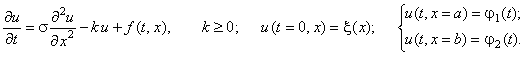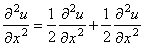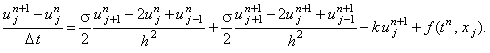Рассмотрим одномерное дифференциальное уравнение параболического типа с начальным и граничными условиями:

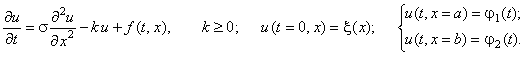(4.17)

Запишем для уравнения (4.17) разностную схему, представляя вторую производную функции u по координате х в виде двух слагаемых и аппроксимируя первое слагаемое на n-ом шаге по времени, а второе - на (n + 1)-ом шаге по времени:

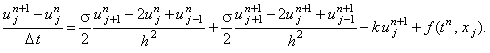(4.18)

Данная разностная схема называется разностной схемой Кранка-Николсона в честь авторов, создавших её.
     Разложение второй производной функции u по координате х на две равноценные составляющие, одна из которых аппроксимируется на n-ом шаге по времени, а другая - на (n + 1)-ом шаге по времени, указывает на то, что аппроксимацию этой производной в целом следует рассматривать на шаге по времени (n + 1/2). В то же время конечная разность, аппроксимирующая производную функции u по времени, по отношению к точке (n + 1/2) является центральной конечной разностью, имеющей, как известно, второй порядок аппроксимации. Следовательно, разностная схема Кранка-Николсона аппроксимирует уравнение (4.17) со вторым порядком и по времени, и по координате: Таким образом, порядок аппроксимации разностной схемы Кранка-Николсона выше, чем порядок аппроксимации явной и неявной разностных схем; то есть, результаты, получаемые при использовании разностной схемы Кранка-Николсона будут более точными.