Рассмотрим одномерное дифференциальное уравнение параболического типа с начальным и граничными условиями:

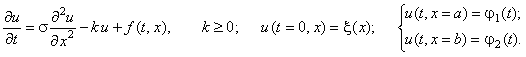(4.19)

Представим разностный оператор для аппроксимации второй производной функции u по координате х (2.12) в следующем виде:

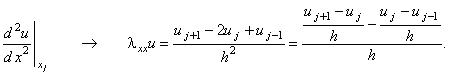(4.20)

Аппроксимируя первую дробь числителя в выражении (4.20) на n-ом шаге по времени, а вторую дробь и свободный член в уравнении (4.19) - на (n + 1)-ом шаге по времени, получим соотношение или, упрощая,

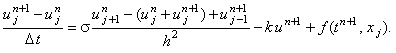(4.21)

      Соотношение (4.21) не аппроксимирует исходное дифференциальное уравнение (4.19). Поэтому рассмотрим следующий шаг по времени на разностной сетке: Аппроксимируя на этот раз первую дробь числителя в выражении (4.20) на (n + 2)-ом шаге по времени, а вторую дробь и свободный член в уравнении (4.19) - на (n + 1)-ом шаге по времени, получим соотношение или, упрощая,

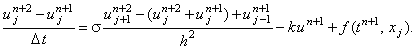(4.22)

Соотношение (4.22) также не аппроксимирует исходное дифференциальное уравнение (4.19). Однако в совокупности выражения (4.21) и (4.22) составляют разностную схему, называемую в честь её автора, разностной схемой Саульева. Сами выражения (4.21) и (4.22) называют первой и второй ступенями разностной схемы Саульева, соответственно.