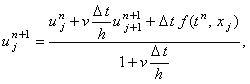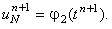|
5.2. Метод решения.
Рассмотрим метод решения разностной схемы (5.4).
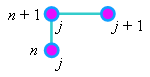
Разностный шаблон (см. рисунок), характеризующий данную разностную схему,
свидетельствует о том, что она содержит две неизвестные величины - значения функции u на
(n + 1)-ом шаге по времени 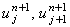 . То есть, для определения величины . То есть, для определения величины 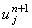 необходимо знать
значение функции u в соседней справа точке на разностной сетке. необходимо знать
значение функции u в соседней справа точке на разностной сетке.
Выражая 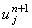 из разностной схемы (5.4), получаем рекуррентное соотношение из разностной схемы (5.4), получаем рекуррентное соотношение
| |
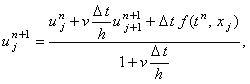 |
(5.9) |
позволяющее последовательно рассчитать все значения функции u на (n + 1)-ом шаге
по времени 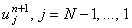 , если известна величина , если известна величина 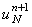 ,
которую можно определить из правого граничного условия:
Таким образом, неявная разностная схема (5.4) по сложности
метода решения не уступает соответствующей явной разностной схеме (5.2), а в отношении устойчивости
имеет очевидное преимущество. Основываясь на этом, мы рекомендуем для численного решения
дифференциального уравнения в частных производных 1-го порядка (5.1) при отрицательном значении
параметра v именно неявную разностную схему с аппроксимацией производной по координате правой
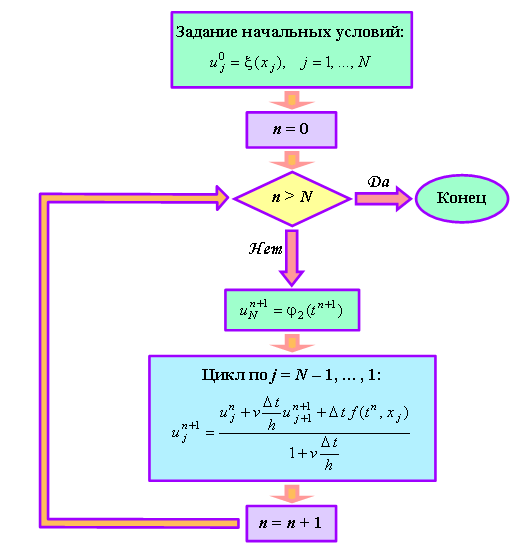
конечной разностью (5.4). Ниже приводится алгоритм её решения (в виде блок-схемы). ,
которую можно определить из правого граничного условия:
Таким образом, неявная разностная схема (5.4) по сложности
метода решения не уступает соответствующей явной разностной схеме (5.2), а в отношении устойчивости
имеет очевидное преимущество. Основываясь на этом, мы рекомендуем для численного решения
дифференциального уравнения в частных производных 1-го порядка (5.1) при отрицательном значении
параметра v именно неявную разностную схему с аппроксимацией производной по координате правой
конечной разностью (5.4). Ниже приводится алгоритм её решения (в виде блок-схемы).
|
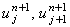 . То есть, для определения величины
. То есть, для определения величины 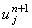 необходимо знать
значение функции u в соседней справа точке на разностной сетке.
необходимо знать
значение функции u в соседней справа точке на разностной сетке.
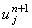 из разностной схемы (5.4), получаем рекуррентное соотношение
из разностной схемы (5.4), получаем рекуррентное соотношение
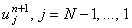 , если известна величина
, если известна величина 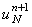 ,
которую можно определить из правого граничного условия:
,
которую можно определить из правого граничного условия: