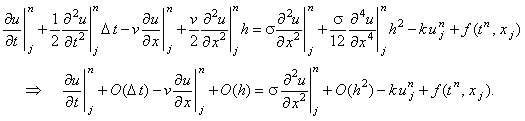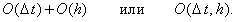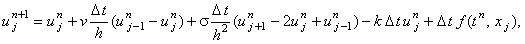|
2.2. Порядок аппроксимации. Метод решения.
Для определения порядка аппроксимации явной разностной схемы (6.2) подставим в неё
выражения (2.16)-(2.18), описывающие разложение значений 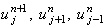 в ряд Тейлора относительно точки
в ряд Тейлора относительно точки 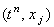 на разностной сетке: на разностной сетке:
Так как ошибка O(h) является более грубой, чем 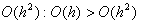 , явная разностная схема (6.2) аппроксимирует исходное
дифференциальное уравнение (6.1) с первым порядком и по времени, и по координате: , явная разностная схема (6.2) аппроксимирует исходное
дифференциальное уравнение (6.1) с первым порядком и по времени, и по координате:
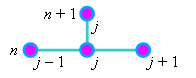
Разностный шаблон
(см. рисунок), характеризующий явную разностную схему (6.2), свидетельствует о том, что она содержит
одну неизвестную величину - значение функции u на (n + 1)-ом шаге по времени.
Выражая эту величину из разностной схемы, получаем рекуррентное соотношение
| |
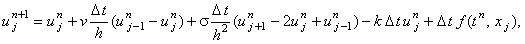 |
(6.4) |
позволяющее рассчитать все значения функции u на (n + 1)-ом шаге по времени
(при известных значениях функции u на n-ом шаге), кроме значений 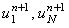 ,
определяемых с помощью граничных условий. Если заданы граничные условия 1-го рода,
то значения ,
определяемых с помощью граничных условий. Если заданы граничные условия 1-го рода,
то значения 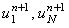 определяются непосредственно из их разностной аппроксимации; если 2-го или 3-го рода,
то - с помощью соотношений (4.4a) и (4.4b). Таким образом, алгоритм решения явной разностной схемы (6.2)
аналогичен алгоритму решения явной разностной схемы (4.2), аппроксимирующей дифференциальное
уравнение параболического типа, не содержащее производную по координате первого порядка. определяются непосредственно из их разностной аппроксимации; если 2-го или 3-го рода,
то - с помощью соотношений (4.4a) и (4.4b). Таким образом, алгоритм решения явной разностной схемы (6.2)
аналогичен алгоритму решения явной разностной схемы (4.2), аппроксимирующей дифференциальное
уравнение параболического типа, не содержащее производную по координате первого порядка.
|
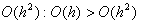 , явная разностная схема (6.2) аппроксимирует исходное
дифференциальное уравнение (6.1) с первым порядком и по времени, и по координате:
, явная разностная схема (6.2) аппроксимирует исходное
дифференциальное уравнение (6.1) с первым порядком и по времени, и по координате:
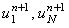 ,
определяемых с помощью граничных условий. Если заданы граничные условия 1-го рода,
то значения
,
определяемых с помощью граничных условий. Если заданы граничные условия 1-го рода,
то значения 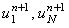 определяются непосредственно из их разностной аппроксимации; если 2-го или 3-го рода,
то - с помощью соотношений (4.4a) и (4.4b). Таким образом, алгоритм решения явной разностной схемы (6.2)
аналогичен алгоритму решения явной разностной схемы (4.2), аппроксимирующей дифференциальное
уравнение параболического типа, не содержащее производную по координате первого порядка.
определяются непосредственно из их разностной аппроксимации; если 2-го или 3-го рода,
то - с помощью соотношений (4.4a) и (4.4b). Таким образом, алгоритм решения явной разностной схемы (6.2)
аналогичен алгоритму решения явной разностной схемы (4.2), аппроксимирующей дифференциальное
уравнение параболического типа, не содержащее производную по координате первого порядка.
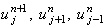 в ряд Тейлора относительно точки
в ряд Тейлора относительно точки 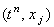 на
на