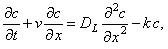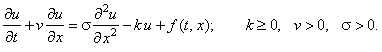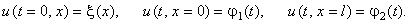В разделе "Примеры математических моделей, содержащих дифференциальные уравнения в частных производных" мы рассматривали математическую модель трубчатого реактора с продольным перемешиванием, в котором протекает простая необратимая реакция. Баланс по концентрации исходного реагента для нестационарного режима имеет вид: где k - константа скорости химической реакции; с - концентрация исходного реагента; v - линейная скорость потока; х - координата по длине реактора; D_L - коэффициент диффузии.
     Данное уравнение относится к дифференциальным уравнениям параболического типа. Однако оно отличается от уже изученных нами уравнений параболического типа наличием первой производной по координате. Рассмотрим влияние этой производной на характеристики и методику решения разностных схем, аппроксимирующих одномерное дифференциальное уравнение параболического типа.

     Для простоты дальнейшего изложения мы будем рассматривать одномерные дифференциальные уравнения параболического типа, содержащие производную по координате первого порядка, в следующем общем виде:

(6.1)

Значение параметра v в общем случае может быть положительным или отрицательным. Напомним, что согласно правилу выбора конечной разности для аппроксимации производной первого порядка по координате при положительном v следует использовать левую конечную разность, при отрицательном v - правую конечную разность. Поэтому рассмотрим только случай v > 0 (случай v < 0 будет аналогичным при аппроксимации первой производной по координате левой конечной разностью). Также отдельно рассмотрим случай аппроксимации производной по координате первого порядка центральной конечной разностью.
     Уравнение (6.1) следует дополнить начальным и граничными условиями (для определённости будем рассматривать граничные условия 1-го рода):