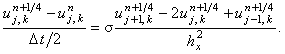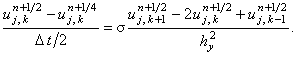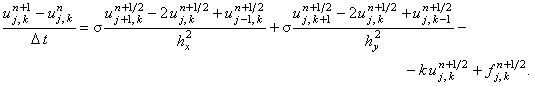|
9.1. Методика записи уравнений схемы.
Рассмотрим ещё одну интерпретацию неявной разностной схемы (7.3),
позволяющую (как и в случае схемы переменных направлений) добиться повышения порядка аппроксимации
по времени, - схему предиктор-корректор.
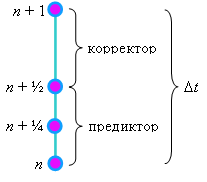
Данная схема требует особого способа расщепления интервала 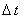 (см. рисунок): интервал
(см. рисунок): интервал 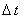 между точками между точками
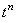 и и 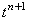 на разностной сетке
расщепляется пополам (полученная промежуточная точка обозначена, как на разностной сетке
расщепляется пополам (полученная промежуточная точка обозначена, как 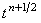 );
интервал );
интервал 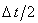 между точками между точками 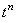 и
и 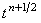 снова расщепляется пополам (полученная промежуточная точка обозначена,
как снова расщепляется пополам (полученная промежуточная точка обозначена,
как 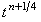 ). ).
На первом полушаге интервала 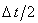 записывается неявная разностная схема,
в которой учитывается только производная второго порядка по координате x: записывается неявная разностная схема,
в которой учитывается только производная второго порядка по координате x:
| |
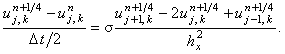 |
(7.15) |
На втором полушаге интервала 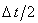 записывается неявная разностная схема, в которой учитывается только производная второго порядка по
координате y:
записывается неявная разностная схема, в которой учитывается только производная второго порядка по
координате y:
| |
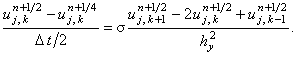 |
(7.16) |
Результатом последовательного решения подсхем (7.15), (7.16), называемых
в совокупности предиктором, являются значения функции u на шаге по времени (n + 1/2).
Для завершения расчётов на всём интервале 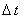 используется поправочное разностное соотношение,
называемое корректором: используется поправочное разностное соотношение,
называемое корректором:
| |
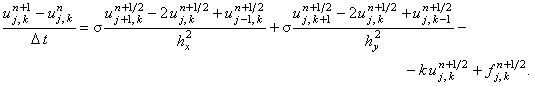 |
(7.17) |
Таким образом, схема предиктор-корректор в случае двумерных задач состоит из трёх подсхем.
|
 (см. рисунок): интервал
(см. рисунок): интервал 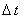 между точками
между точками
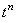 и
и 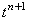 на разностной сетке
расщепляется пополам (полученная промежуточная точка обозначена, как
на разностной сетке
расщепляется пополам (полученная промежуточная точка обозначена, как 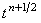 );
интервал
);
интервал 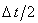 между точками
между точками 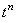 и
и 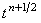 снова расщепляется пополам (полученная промежуточная точка обозначена,
как
снова расщепляется пополам (полученная промежуточная точка обозначена,
как 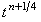 ).
).
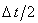 записывается неявная разностная схема,
в которой учитывается только производная второго порядка по координате x:
записывается неявная разностная схема,
в которой учитывается только производная второго порядка по координате x:
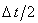 записывается неявная разностная схема, в которой учитывается только производная второго порядка по
координате y:
записывается неявная разностная схема, в которой учитывается только производная второго порядка по
координате y:
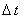 используется поправочное разностное соотношение,
называемое корректором:
используется поправочное разностное соотношение,
называемое корректором: