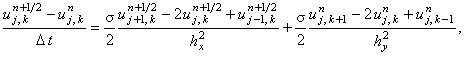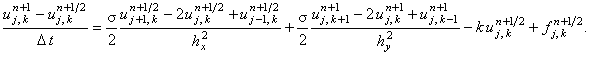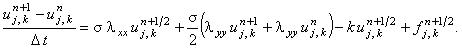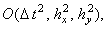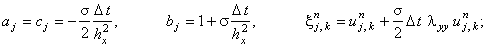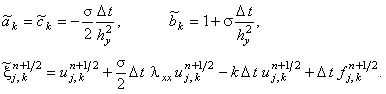7. Схема переменных направлений.
|
Рассмотрим способ интерпретации неявной разностной схемы (7.3), позволяющий добиться повышения порядка аппроксимации по времени, - схему переменных направлений:
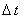 и является неявной по координате x и явной по координате y. Вторая подсхема
аппроксимируется на втором полушаге интервала
и является неявной по координате x и явной по координате y. Вторая подсхема
аппроксимируется на втором полушаге интервала 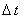 и является неявной по координате y и
явной по координате x. Каждая из подсхем (как и в случае схемы расщепления (7.7), (7.8))
является абсолютно устойчивой и решается с помощью метода прогонки. и является неявной по координате y и
явной по координате x. Каждая из подсхем (как и в случае схемы расщепления (7.7), (7.8))
является абсолютно устойчивой и решается с помощью метода прогонки.
Обратим внимание на две особенности, которые необходимо учитывать при записи схемы переменных направлений (7.13): 1) коэффициенты перед разностными операторами, аппроксимирующими производные 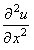 и и 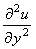 , должны быть поделены пополам;
2) свободный член записывается во второй подсхеме и аппроксимируется на шаге (n + 1/2). , должны быть поделены пополам;
2) свободный член записывается во второй подсхеме и аппроксимируется на шаге (n + 1/2).
Складывая обе подсхемы и принимая во внимание обозначения (7.6), получаем:
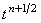 . Это означает,
что разностный оператор в левой части является центральной конечной разностью, которая, как известно,
имеет второй порядок аппроксимации. Таким образом, схема переменных направлений (7.13), имея порядок
аппроксимации . Это означает,
что разностный оператор в левой части является центральной конечной разностью, которая, как известно,
имеет второй порядок аппроксимации. Таким образом, схема переменных направлений (7.13), имея порядок
аппроксимации
Алгоритм решения схемы переменных направлений (7.13) аналогичен алгоритму решения схемы расщепления (7.7), (7.8). Коэффициенты, соответствующие уравнению (4.10), имеют вид: для первой подсхемы
для второй подсхемы
|