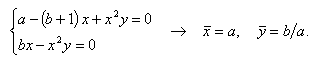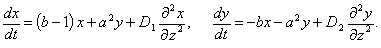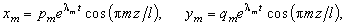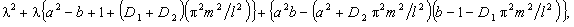(на примере реакционной схемы в реакторах идеального смешения и трубчатого)
3. Пространственная самоорганизация
|
3.2. Исследование устойчивости однородных стационарных состояний системы
Определим простые решения системы уравнений (12.6), т.е. стационарные и однородные по пространству. При этом все производные в (12.6) будут равны нулю, и мы получим систему обычных алгебраических уравнений, имеющую единственное решение:
Проведём линеаризацию системы уравнений (12.6) и получим линейную задачу:
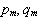 - амплитуды гармоники с номером m, - амплитуды гармоники с номером m,
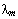 - экспоненциальный множитель. - экспоненциальный множитель.
Подставив выражения (12.8) в уравнения (12.7), можно убедиться, что эти функции будут решениями, если 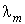 удовлетворяют квадратным уравнениям: удовлетворяют квадратным уравнениям:
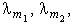 которые являются комплексными числами. которые являются комплексными числами.
Если 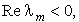 то решение (12.8) убывает со временем (напомним, что для линеаризованных уравнений под функциями х и у понимаются возмущения концентраций веществ Х и У вблизи однородного стационарного состояния).
Если
то решение (12.8) убывает со временем (напомним, что для линеаризованных уравнений под функциями х и у понимаются возмущения концентраций веществ Х и У вблизи однородного стационарного состояния).
Если 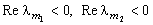 для всех m, то однородное стационарное состояние, к которому с течением времени стремится система, устойчиво. Данное условие устойчивости выполняется при малых b. для всех m, то однородное стационарное состояние, к которому с течением времени стремится система, устойчиво. Данное условие устойчивости выполняется при малых b.
Если при некотором 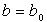 действительные части действительные части 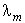 обращаются в нуль: обращаются в нуль:
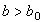 однородное стационарное состояние теряет устойчивость и в системе возникают структуры и колебания концентраций веществ Х и У в пространстве. однородное стационарное состояние теряет устойчивость и в системе возникают структуры и колебания концентраций веществ Х и У в пространстве.
|