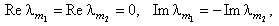(на примере реакционной схемы в реакторах идеального смешения и трубчатого)
3. Пространственная самоорганизация
|
3.3.Возникновение диссипативных структур
Таким образом, решая обычные квадратичные уравнения, мы можем узнать, когда в нелинейной среде возникнут диссипативные структуры.
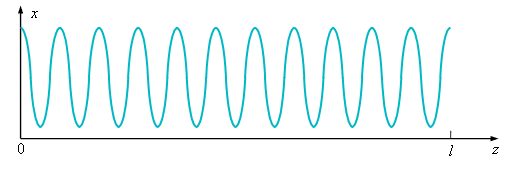
Анализ уравнения (12.7) позволяет предсказать колебательные режимы. Если при
Модель "брюсселятор" является одной из самых известных математических моделей в нелинейной динамике. Название её связано с тем, что она была предложена брюссельской научной школой. И хотя эта модель описывает распределение реагентов в пространстве и во времени для сравнительно узкого класса химических реакций, при её исследовании были выяснены свойства диссипативных структур во многих открытых нелинейных системах, далёких от равновесия. |
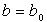 для некоторого значения m выполняются условия:
для некоторого значения m выполняются условия: