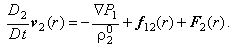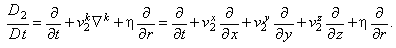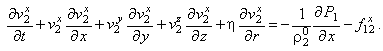4. Уравнение движения дисперсной фазы
|
Уравнение сохранения импульса для дисперсной r-фазы имеет вид:
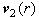 - средняя массовая скорость r-фазы; - средняя массовая скорость r-фазы;
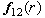 - сила взаимодействия между сплошной фазой и r-фазой,
возникающая вследствие действия сил трения при контакте фаз; Р - давление; - сила взаимодействия между сплошной фазой и r-фазой,
возникающая вследствие действия сил трения при контакте фаз; Р - давление;
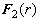 - массовые силы, действующие на включения размером r,
отнесённые к единице массы включений (т.е. истинной плотности - массовые силы, действующие на включения размером r,
отнесённые к единице массы включений (т.е. истинной плотности 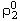 ). ).
Первое слагаемое в правой части уравнения (2.6) характеризует влияние поверхностных сил, действующих на r-фазу; второе слагаемое - влияние сил трения между сплошной фазой и включениями размера r; третье слагаемое - воздействие массовых сил. Отметим, что как и уравнение баланса числа включений (2.2), уравнение (2.6) записано для r-фазы. Для получения уравнения движения всей дисперсной фазы надо умножить каждый член уравнения (2.6) на 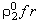 и проинтегрировать его по dr от 0 до R (где R - наибольший размер включений). и проинтегрировать его по dr от 0 до R (где R - наибольший размер включений).
Обозначение 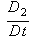 означает субстанциональную производную: означает субстанциональную производную:
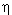 - наблюдаемая скорость изменения размера включения). - наблюдаемая скорость изменения размера включения).
С учётом выражений (2.7) и (2.5) уравнение движения r-фазы (2.6) можно записать в проекциях на оси координат. Например, в проекции на ось х оно будет иметь вид:
|