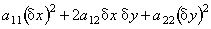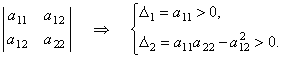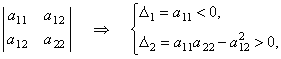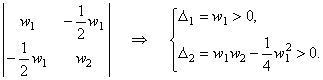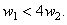Согласно второму методу Ляпунова знак производной второй вариации энтропии определяет устойчивость стационарных состояний систем, удалённых от равновесия: если эта величина положительна, то стационарное состояние системы устойчиво, если - отрицательна, то - неустойчиво. В то же время производная второй вариации энтропии системы является квадратичной формой, что позволяет исследовать её знак с помощью критерия Сильвестра.
     Критерий Сильвестра. Для того, чтобы квадратичная форма была положительно определена, необходимо и достаточно, чтобы все главные диагональные миноры матрицы квадратичной формы были строго положительны: Если же знаки главных диагональных миноров матрицы квадратичной формы чередуются, причём первый из них отрицателен то данная квадратичная форма является отрицательно определённой.

     С помощью критерия Сильвестра определим, при каких условиях квадратичная форма (6.8) является положительно определённой. Составим для неё матрицу квадратичной формы и определим главные диагональные миноры этой матрицы: Первое условие выполняется автоматически. Из второго условия получаем: Таким образом, гарантировать положительный знак производной термодинамической функции Ляпунова для рассматриваемого реакционного процесса (т.е. его устойчивость) можно только при выполнении данного соотношения между скоростями его стадий.