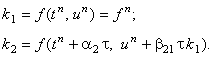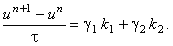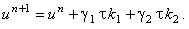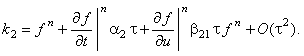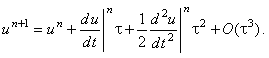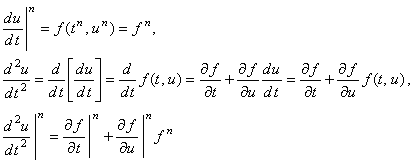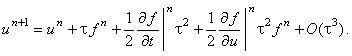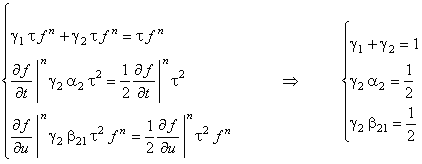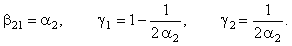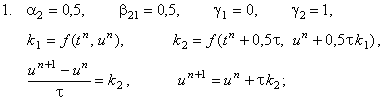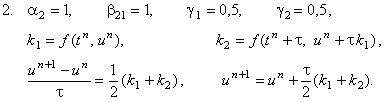|
Заменим в выражении для k2 (12.7) коэффициенты при 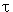 неизвестными параметрами
неизвестными параметрами 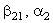 : :
Разностную схему для уравнения (12.1) представим в виде:
Тогда решение на (n + 1)-ом шаге по времени будет определяться рекуррентным соотношением:
| |
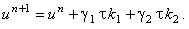 |
(12.8) |
Разложим функцию k2 в ряд Тейлора:
Подставим данное выражение в рекуррентное соотношение (12.8):
| |
 |
(12.9) |
Разложим функцию 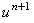 в ряд Тейлора:
Данная формула с учётом равенств
примет следующий вид: в ряд Тейлора:
Данная формула с учётом равенств
примет следующий вид:
| |
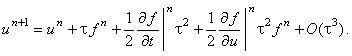 |
(12.10) |
Сравнивая соотношения (12.9) и (12.10), получаем следующую систему уравнений:
| |
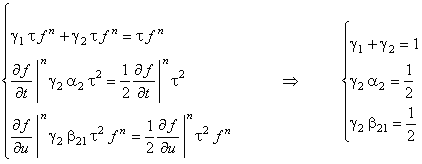 |
(12.11) |
Система (12.11) состоит из трёх уравнений с четырьмя неизвестными, поэтому она не может иметь
однозначного решения. Для определения значений неизвестных параметров необходимо задать значение
одного из них (обычно задают значение параметра  ); тогда значения остальных параметров можно
определить из уравнений системы (12.11):
По этой причине принято говорить не о методе Рунге-Кутта второго порядка, а о семействе методов
Рунге-Кутта второго порядка, поскольку в зависимости от выбранного значения параметра ); тогда значения остальных параметров можно
определить из уравнений системы (12.11):
По этой причине принято говорить не о методе Рунге-Кутта второго порядка, а о семействе методов
Рунге-Кутта второго порядка, поскольку в зависимости от выбранного значения параметра  мы получим тот или иной вид рекуррентного соотношения (12.8).
мы получим тот или иной вид рекуррентного соотношения (12.8).
На практике используются, как правило, два случая:
Видно, что первый случай совпадает с методом Рунге-Кутта второго порядка,
рассмотренным в предыдущем разделе.
|
 в ряд Тейлора:
в ряд Тейлора:
 ); тогда значения остальных параметров можно
определить из уравнений системы (12.11):
); тогда значения остальных параметров можно
определить из уравнений системы (12.11):
 мы получим тот или иной вид рекуррентного соотношения (12.8).
мы получим тот или иной вид рекуррентного соотношения (12.8).
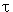 неизвестными параметрами
неизвестными параметрами 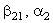 :
: