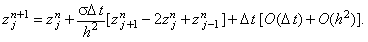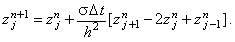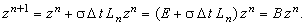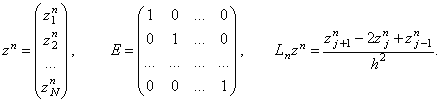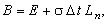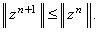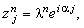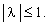|
Выразим из соотношения (3.5) величину погрешности на
(n + 1)-ом шаге по времени:
Последний член в правой части полученного выражения имеет порядок малости,
явно меньший 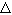 t, что позволяет им пренебречь. Таким образом, получаем:
Представим данное выражение в операторном виде:
Здесь zn - вектор погрешностей, Е - единичный оператор:
Оператор В, определяемый с помощью выражения
называют оператором перехода от n-го шага по времени к (n + 1)-му шагу по времени. t, что позволяет им пренебречь. Таким образом, получаем:
Представим данное выражение в операторном виде:
Здесь zn - вектор погрешностей, Е - единичный оператор:
Оператор В, определяемый с помощью выражения
называют оператором перехода от n-го шага по времени к (n + 1)-му шагу по времени.
Для того чтобы разностная схема (3.4),
аппроксимирующая дифференциальное уравнение (3.3), была устойчива,
необходимо (согласно определению устойчивости разностных схем),
чтобы норма погрешности на (n + 1)-ом шаге по времени не превосходила нормы
погрешности на n-ом шаге по времени, то есть:
| |
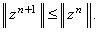 |
(3.6) |
Погрешность решения разностной схемы в точке 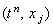 можно представить в виде комплексного выражения (гармоники):
можно представить в виде комплексного выражения (гармоники):
| |
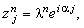 |
(3.7) |
где 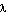 - собственное число оператора перехода В; i - мнимая единица. - собственное число оператора перехода В; i - мнимая единица.
Теорема. Для того,
чтобы разностная схема была устойчива (т.е. для выполнения условия (3.6)), необходимо,
чтобы все собственные числа оператора перехода В удовлетворяли условию:
| |
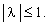 |
(3.8) |
Данное условие является необходимым условием устойчивости разностных схем.
|
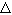 t, что позволяет им пренебречь. Таким образом, получаем:
t, что позволяет им пренебречь. Таким образом, получаем:
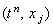 можно представить в виде комплексного выражения (гармоники):
можно представить в виде комплексного выражения (гармоники):
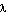 - собственное число оператора перехода В; i - мнимая единица.
- собственное число оператора перехода В; i - мнимая единица.