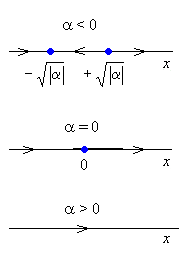Рассмотрим одномерное параметрическое дифференциальное уравнение:

(11.2)

где может принимать значения < 0, > 0, = 0.

     Рассмотрим три случая.

     Случай 1. < 0. Уравнение (11.2) имеет две неподвижные точки: Неподвижная точка является аттрактором, а точка - репеллер (см. рисунок).

     Случай 2. = 0. Уравнение (11.2) имеет одну неподвижную точку которая является шунтом (см. рисунок).

     Случай 3. > 0. Уравнение (11.2) неподвижных точек не имеет (см. рисунок).

     Таким образом, значение = 0 является бифуркационным значением параметра.

     Когда параметр возрастает, приближаясь к 0 слева ( - 0), устойчивая и неустойчивая неподвижные точки приближаются друг к другу, при = 0 они сливаются, а при > 0 одновременно исчезают. Можно сказать, что неподвижные точки при слиянии аннигилируют, взаимно уничтожаются.

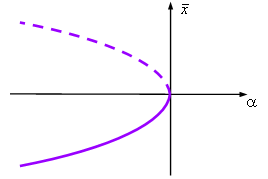
     Более наглядно бифуркацию типа седло-узел можно описать, построив зависимость стационарных решений уравнения (11.2) от параметра (см. рисунок). Данная зависимость имеет вид параболы, причём верхняя её ветвь отображает неустойчивые положения равновесия, а нижняя - устойчивые.

     Реальная система, описываемая уравнением (11.2), стабилизируется в устойчивом состоянии равновесия, так что о существовании другого, неустойчивого, состояния равновесия, как правило, ничего не известно. При переходе параметра через бифуркационное значение = 0 слева направо это устойчивое состояние равновесия внезапно исчезает. Наоборот, если параметр переходит через бифуркационное значение = 0 справа налево, внезапно появляется одно устойчивое состояние равновесия системы. В одномерном случае этот тип бифуркации называется аттрактор-шунт или шунт-аттрактор.