1. Понятие бифуркации
|
Исследуемый реальный процесс протекает обычно при определённых внешних условиях, которые в общем случае можно охарактеризовать определёнными значениями параметров системы. Эти параметры входят также и в соответствующую систему дифференциальных уравнений. Таким образом, математическая модель принимает вид: 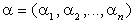 - вектор параметров системы. - вектор параметров системы.
Определение. Качественное изменение фазового портрета, происходящее при изменении параметра системы  ,
называется бифуркацией фазового портрета. Значение параметра системы ,
называется бифуркацией фазового портрета. Значение параметра системы  = =  0, при котором происходит бифуркация,
называется бифуркационным значением параметра (или точкой бифуркации). 0, при котором происходит бифуркация,
называется бифуркационным значением параметра (или точкой бифуркации).Например, имеем уравнение:
 > 0
и распада ядра при > 0
и распада ядра при  < 0.
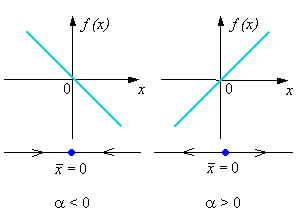
На рисунке представлен фазовый портрет уравнения (11.1) при < 0.
На рисунке представлен фазовый портрет уравнения (11.1) при  < 0
и < 0
и  > 0.
Видно, что при > 0.
Видно, что при  < 0 неподвижная точка < 0 неподвижная точка  > 0 - репеллер.
Когда > 0 - репеллер.
Когда  возрастает, проходя через нуль, то решение из убывающего превращается в возрастающее.
Таким образом, возрастает, проходя через нуль, то решение из убывающего превращается в возрастающее.
Таким образом,  = 0 - точка бифуркации. = 0 - точка бифуркации.
На практике наиболее часто встречаются три типа бифуркаций: бифуркация типа седло-узел, бифуркация Андронова-Хопфа и бифуркация с удвоением периода. |