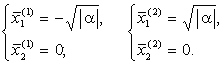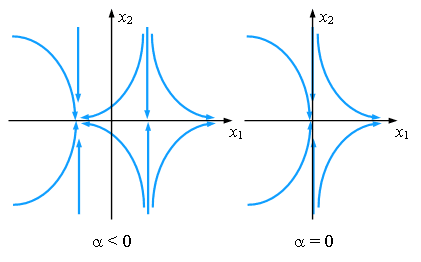Рассмотрим систему уравнений:

(11.3)

     Случай 1. < 0. Система (11.3) имеет две неподвижные точки:

(11.4)

Линеаризуем систему (11.3) в окрестности неподвижных точек (11.4):

	Неподвижная точка 1	Неподвижная точка 2
	0	0
	0	0
	-1	-1

Собственные числа матрицы А равны:

Неподвижная точка 1	Неподвижная точка 2

Следовательно, неподвижная точка 1 - устойчивый узел, а неподвижная точка 2 - седло.

     Случай 2. = 0. Система (11.3) имеет одну неподвижную точку Легко увидеть, что собственные числа матрицы А равны:

     Таким образом, значение = 0 является бифуркационным значением параметра; причём одно из собственных чисел матрицы А при бифуркационном значении параметра равняется нулю.

     На рисунке изображена бифуркация типа седло-узел для рассматриваемого случая. Видно, что при < 0 система имеет две неподвижные точки, одна из которых седло, а другая - устойчивый узел. При 0 они приближаются друг к другу и при = 0 сливаются вместе в так называемое седло-узел. Отсюда и возникло название "бифуркация типа седло-узел".

     В общем n-мерном случае, если для некоторого положения равновесия матрица линеаризации имеет одно собственное число, равное нулю, бифуркация происходит аналогично: при изменении параметра положение равновесия либо исчезает, либо расщепляется на два новых положения равновесия. Это утверждение справедливо почти для всех параметрических систем дифференциальных уравнений с n-мерным фазовым пространством.