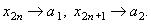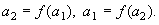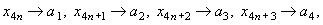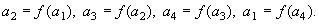1. Бифуркация удвоения периода
|
1.4. Возникновение циклов
При увеличении
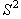 (см. рисунок).
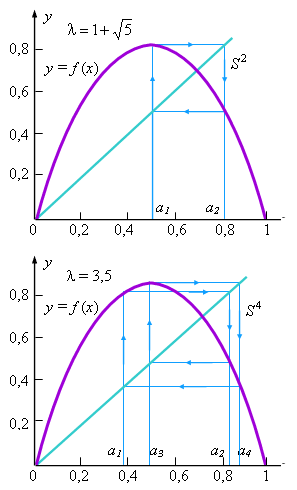
Наличие цикла (см. рисунок).
Наличие цикла 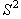 означает,
что численность популяции будет меняться с периодом в 2 характерных интервала. означает,
что численность популяции будет меняться с периодом в 2 характерных интервала.
Переход от неподвижной точки, которую можно считать циклом  ,
к циклу ,
к циклу 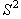 произошёл в результате бифуркации,
называемой бифуркацией удвоения периода. Неподвижная точка произошёл в результате бифуркации,
называемой бифуркацией удвоения периода. Неподвижная точка 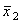 (14.4) при этом не исчезла, однако условие
устойчивости (14.6) для неё перестало выполняться. Значение (14.4) при этом не исчезла, однако условие
устойчивости (14.6) для неё перестало выполняться. Значение  = 3 есть точка бифуркации удвоения периода. = 3 есть точка бифуркации удвоения периода.
При дальнейшем увеличении  в последовательности
в последовательности 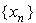 возникает цикл возникает цикл 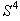 (см. рисунок): (см. рисунок):
Последовательно увеличивая значение параметра  ,
мы получим циклы ,
мы получим циклы 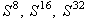 и т. д.
При этом в каждой точке бифуркации цикл и т. д.
При этом в каждой точке бифуркации цикл 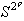 теряет устойчивость, а цикл
теряет устойчивость, а цикл 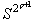 становится устойчивым.
При значении становится устойчивым.
При значении 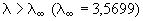 формула (14.2)
даёт уже непериодическую последовательность формула (14.2)
даёт уже непериодическую последовательность 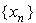 . .
Таким образом, в рассматриваемой системе (14.2) удаётся проследить большое количество бифуркаций, приводящих к усложнению решения. |
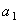 и
и 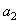 , т.е. при
, т.е. при 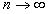 :
: