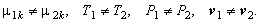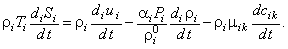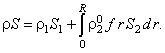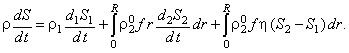1. Термодинамика многофазной гетерогенной среды
|
Рассмотрим многофазную полидисперсную среду, где одна фаза (сплошная, несущая) - газ или жидкость, а другие фазы (дисперсные r-фазы) - включения твёрдых частиц, капель жидкости или газовых пузырьков (подробное описание см. в разделе "Математическое описание многофазной гетерогенной среды"). Смесь в целом неравновесна, но можно допустить, что в каждом локальном объёме смеси существует локальное термодинамическое равновесие внутри каждой из фаз. При этом между самими фазами равновесия не существует даже в локальном объёме смеси, т.е.
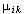 - химический потенциал k-го компонента в i-й фазе; - химический потенциал k-го компонента в i-й фазе;
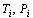 - температура и давление i-й фазы; - температура и давление i-й фазы;
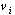 - средняя массовая скорость i-й фазы (i = 1, 2). - средняя массовая скорость i-й фазы (i = 1, 2).
Для каждой из фаз в локальном объёме смеси выполняется [7] соотношение Гиббса:
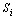 - удельная энтропия
i-й фазы; - удельная энтропия
i-й фазы; 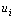 - удельная внутренняя энергия i-й фазы; - удельная внутренняя энергия i-й фазы;
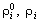 - истинная и средняя плотности i-й фазы; - истинная и средняя плотности i-й фазы;
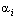 - объёмная доля i-й фазы; - объёмная доля i-й фазы;
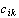 - концентрация k-го компонента в i-й фазе.
Обозначение - концентрация k-го компонента в i-й фазе.
Обозначение 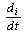 означает субстанциональную производную (2.4), (2.7). означает субстанциональную производную (2.4), (2.7).
Энтропия рассматриваемой системы определяется соотношением:
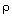 - средняя плотность смеси; - средняя плотность смеси;
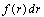 - число включений в единице объёма смеси с размером от r до r + dr; R - наибольший размер включений. - число включений в единице объёма смеси с размером от r до r + dr; R - наибольший размер включений.
Изменение энтропии многофазной полидисперсной среды во времени [6] имеет вид:
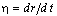 - наблюдаемая скорость изменения размера включения. - наблюдаемая скорость изменения размера включения.
|