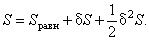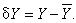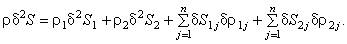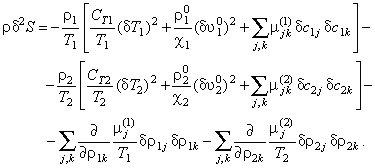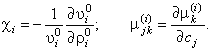|
Согласно второму началу термодинамики (1.1) состояние равновесия изолированной системы
устойчиво, если оно соответствует максимуму энтропии. Энтропию системы, находящейся вблизи равновесного состояния,
можно представить в виде:
| |
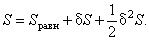 |
(5.1) |
Здесь 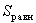 - значение энтропии в состоянии равновесия; - значение энтропии в состоянии равновесия;
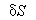 и и 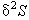 - первая и вторая вариации энтропии системы.
Под вариацией какого-либо параметра Y понимают отклонение величины этого параметра от его стационарного или
равновесного значения - первая и вторая вариации энтропии системы.
Под вариацией какого-либо параметра Y понимают отклонение величины этого параметра от его стационарного или
равновесного значения 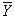 под воздействием внешних возмущений:
Поскольку под воздействием внешних возмущений:
Поскольку 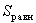 является максимальным значением
энтропии, член первого порядка является максимальным значением
энтропии, член первого порядка 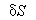 обращается
в нуль, и следовательно, устойчивость состояния системы, находящейся вблизи равновесия, определяется знаком члена
второго порядка обращается
в нуль, и следовательно, устойчивость состояния системы, находящейся вблизи равновесия, определяется знаком члена
второго порядка 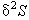 . Таким образом, в области,
близкой к равновесию, . Таким образом, в области,
близкой к равновесию, 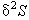 играет роль функции Ляпунова. играет роль функции Ляпунова.
Для многофазной гетерогенной среды, в которой могут происходить химические и
фазовые превращения, вторая вариация энтропии имеет вид:
Здесь 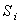 - удельная энтропия
i-й фазы (i = 1,2); - удельная энтропия
i-й фазы (i = 1,2); 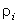 - средняя плотность i-й фазы; - средняя плотность i-й фазы;
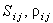 - энтропия и средняя плотность j-го компонента в i-й фазе. - энтропия и средняя плотность j-го компонента в i-й фазе.
С помощью ряда преобразований [6], это выражение можно представить в виде квадратичной формы:
| |
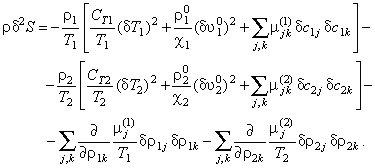 |
(5.2) |
Здесь 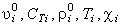 - удельный объём, теплоёмкость,
истинная плотность, температура и коэффициент сжимаемости i-й фазы (i = 1,2),
соответственно; - удельный объём, теплоёмкость,
истинная плотность, температура и коэффициент сжимаемости i-й фазы (i = 1,2),
соответственно; 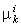 - химический потенциал k-го компонента
в i-й фазе; - химический потенциал k-го компонента
в i-й фазе;
|
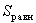 - значение энтропии в состоянии равновесия;
- значение энтропии в состоянии равновесия;
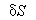 и
и 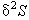 - первая и вторая вариации энтропии системы.
Под вариацией какого-либо параметра Y понимают отклонение величины этого параметра от его стационарного или
равновесного значения
- первая и вторая вариации энтропии системы.
Под вариацией какого-либо параметра Y понимают отклонение величины этого параметра от его стационарного или
равновесного значения 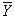 под воздействием внешних возмущений:
под воздействием внешних возмущений:
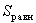 является максимальным значением
энтропии, член первого порядка
является максимальным значением
энтропии, член первого порядка 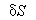 обращается
в нуль, и следовательно, устойчивость состояния системы, находящейся вблизи равновесия, определяется знаком члена
второго порядка
обращается
в нуль, и следовательно, устойчивость состояния системы, находящейся вблизи равновесия, определяется знаком члена
второго порядка 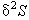 . Таким образом, в области,
близкой к равновесию,
. Таким образом, в области,
близкой к равновесию, 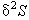 играет роль функции Ляпунова.
играет роль функции Ляпунова.
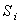 - удельная энтропия
i-й фазы (i = 1,2);
- удельная энтропия
i-й фазы (i = 1,2); 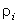 - средняя плотность i-й фазы;
- средняя плотность i-й фазы;
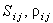 - энтропия и средняя плотность j-го компонента в i-й фазе.
- энтропия и средняя плотность j-го компонента в i-й фазе.
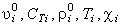 - удельный объём, теплоёмкость,
истинная плотность, температура и коэффициент сжимаемости i-й фазы (i = 1,2),
соответственно;
- удельный объём, теплоёмкость,
истинная плотность, температура и коэффициент сжимаемости i-й фазы (i = 1,2),
соответственно; 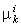 - химический потенциал k-го компонента
в i-й фазе;
- химический потенциал k-го компонента
в i-й фазе;