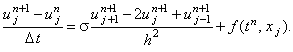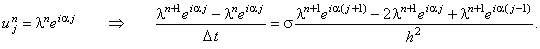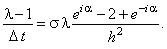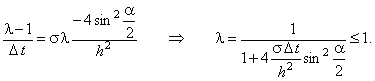Рассмотрим неявную разностную схему, аппроксимирующую дифференциальное уравнение (3.3): Можно доказать, что разностная схема для погрешности решения в этом случае (как и в случае явной разностной схемы), по структуре совпадает с неявной разностной схемой для однородного уравнения параболического типа. Поэтому для исследования устойчивости неявной разностной схемы отбрасываем свободный член и представляем решение в виде гармоники (3.7) (по аналогии с тем, как это было сделано для явной разностной схемы): Далее, упрощаем полученное выражение, деля левую и правую его части на 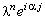: Используя зависимости (3.9), (3.10), получаем формулу, из которой затем выражаем : Легко видеть, что необходимое условие устойчивости разностных схем (3.8) в данном случае выполняется при любых значениях 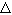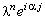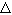t и h. Такие разностные схемы, устойчивость которых не зависит от выбора интервала деления на разностной сетке, называют абсолютно устойчивыми.