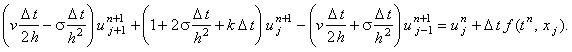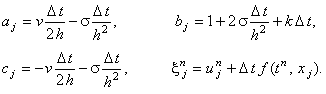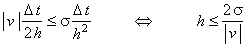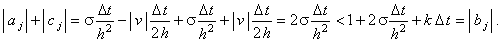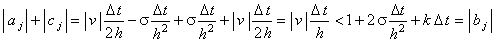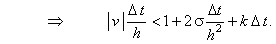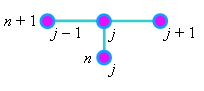
Разностный шаблон (см. рисунок), характеризующий разностную схему (6.8), свидетельствует о том, что она содержит три неизвестные величины - значения функции u на (n + 1)-ом шаге по времени. Следовательно, для решения данной разностной схемы необходимо использовать метод прогонки.
     Приведём разностную схему (6.8) к виду (4.10), удобному для использования метода прогонки: Следовательно, коэффициенты, соответствующие уравнению (4.10), имеют вид: Легко видеть, что для случая

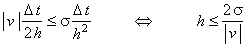(6.9)

достаточное условие сходимости прогонки (4.16) для разностной схемы (6.8) выполняется: Если же то достаточное условие сходимости прогонки (4.16) для разностной схемы (6.8) выполняется только в случае справедливости неравенства:

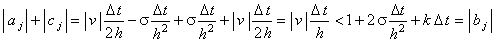
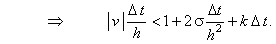
(6.10)

Таким образом, если величина шага по координате удовлетворяет условию (6.9), то ограничений на шаг по времени нет; если же величина шага по координате не удовлетворяет условию (6.9), то при выборе шага по времени необходимо учитывать условие (6.10). Отметим, что если условие (6.9) позволяет задать приемлемую величину шага по координате (h = 0,1), то разностная схема (6.8) становится более предпочтительной по сравнению с разностной схемой (6.5) в силу большего порядка аппроксимации по координате.
     Алгоритм решения, а также методики определения прогоночных коэффициентов и решения на правой границе аналогичны описанным ранее.