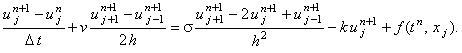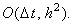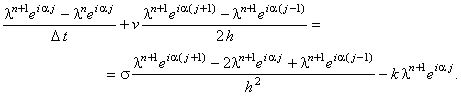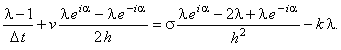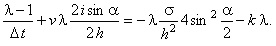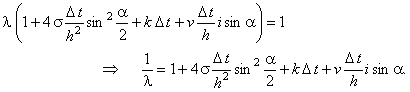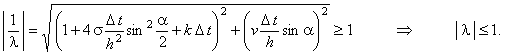|
5.1. Характеристика.
Неявная разностная схема для уравнения (6.1) при аппроксимации
производной по координате первого порядка центральной конечной разностью имеет вид:
| |
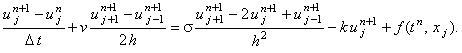 |
(6.8) |
Учитывая порядок аппроксимации разностных операторов, составляющих данную разностную схему, легко видеть,
что она аппроксимирует дифференциальное уравнение (6.1) с первым порядком по времени,
и со вторым - по координате:
Исследуем устойчивость разностной схемы (6.8) с помощью спектрального метода.
Для этого отбрасываем член 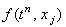 , наличие которого, как известно,
не оказывает влияния на устойчивость разностной схемы, и представляем решение в виде гармоники (3.7):
Далее, упрощаем полученное выражение, деля левую и правую его части на , наличие которого, как известно,
не оказывает влияния на устойчивость разностной схемы, и представляем решение в виде гармоники (3.7):
Далее, упрощаем полученное выражение, деля левую и правую его части на 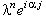 :
Используя зависимости (3.9), (3.10), получаем
Группируя члены, содержащие :
Используя зависимости (3.9), (3.10), получаем
Группируя члены, содержащие  ,
в левой части уравнения, выразим величину, обратную ,
в левой части уравнения, выразим величину, обратную  :
Определим модуль полученного комплексного числа:
Таким образом, собственные числа оператора перехода, удовлетворяют условию устойчивости разностных схем (3.8).
Следовательно, неявная разностная схема с аппроксимацией производной по координате первого порядка
центральной конечной разностью (6.8) абсолютно устойчива, причём вне зависимости от знака параметра v. :
Определим модуль полученного комплексного числа:
Таким образом, собственные числа оператора перехода, удовлетворяют условию устойчивости разностных схем (3.8).
Следовательно, неявная разностная схема с аппроксимацией производной по координате первого порядка
центральной конечной разностью (6.8) абсолютно устойчива, причём вне зависимости от знака параметра v.
|
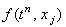 , наличие которого, как известно,
не оказывает влияния на устойчивость разностной схемы, и представляем решение в виде гармоники (3.7):
, наличие которого, как известно,
не оказывает влияния на устойчивость разностной схемы, и представляем решение в виде гармоники (3.7):
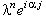 :
:
 ,
в левой части уравнения, выразим величину, обратную
,
в левой части уравнения, выразим величину, обратную  :
: