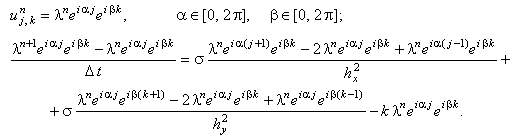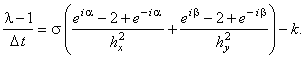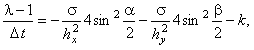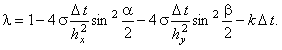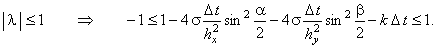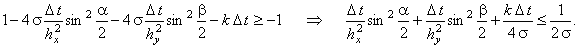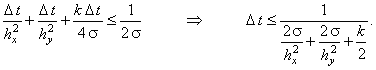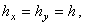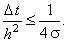|
4.1. Исследование устойчивости.
Исследуем устойчивость явной разностной схемы (7.2), аппроксимирующей
дифференциальное уравнение (7.1), с помощью спектрального метода. Для этого отбрасываем член 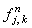 ,
наличие которого, как известно, не оказывает влияния на устойчивость разностной схемы,
и представляем решение в виде гармоники: ,
наличие которого, как известно, не оказывает влияния на устойчивость разностной схемы,
и представляем решение в виде гармоники:
Далее, упрощаем полученное выражение, деля левую и правую его части на 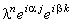 :
Используя зависимости (3.9), (3.10), получаем формулу
из которой выражаем :
Используя зависимости (3.9), (3.10), получаем формулу
из которой выражаем  :
С учётом необходимого условия устойчивости разностных схем (3.8) имеем:
В полученном двойном неравенстве правое условие выполняется автоматически. Поэтому рассмотрим
более подробно левое условие:
Данное выражение содержит две переменные величины - :
С учётом необходимого условия устойчивости разностных схем (3.8) имеем:
В полученном двойном неравенстве правое условие выполняется автоматически. Поэтому рассмотрим
более подробно левое условие:
Данное выражение содержит две переменные величины -  и и 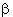 .
Чтобы гарантировать устойчивость разностной схемы (7.2) независимо от значений этих величин, следует перейти к более строгому условию,
задавая для .
Чтобы гарантировать устойчивость разностной схемы (7.2) независимо от значений этих величин, следует перейти к более строгому условию,
задавая для 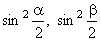 максимально возможное значение, равное 1: максимально возможное значение, равное 1:
| |
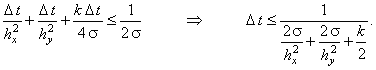 |
(7.4) |
Выражение (7.4) является условием устойчивости явной разностной схемы (7.2), аппроксимирующей
дифференциальное уравнение (7.1). В случае отсутствия в уравнении (7.1) свободного члена
(т.е. при k = 0), а также если интервалы между точками по осям х и y на
разностной сетке задать равными
выражение (7.4) примет более простой вид:
| |
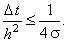 |
(7.4a) |
Сравнивая данное выражение с соотношением (3.12) (являющимся условием устойчивости явной разностной
схемы (3.4), аппроксимирующей одномерное дифференциальное уравнение параболического типа (3.3)) можно
сделать вывод, что увеличение размерности системы на порядок приводит к уменьшению в два раза
максимально возможного значения 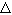 t, при котором явная разностная схема будет устойчива. t, при котором явная разностная схема будет устойчива.
|
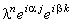 :
:
 :
:
 и
и 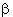 .
Чтобы гарантировать устойчивость разностной схемы (7.2) независимо от значений этих величин, следует перейти к более строгому условию,
задавая для
.
Чтобы гарантировать устойчивость разностной схемы (7.2) независимо от значений этих величин, следует перейти к более строгому условию,
задавая для 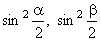 максимально возможное значение, равное 1:
максимально возможное значение, равное 1:
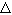 t, при котором явная разностная схема будет устойчива.
t, при котором явная разностная схема будет устойчива.
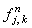 ,
наличие которого,
,
наличие которого,