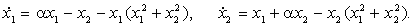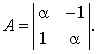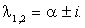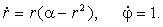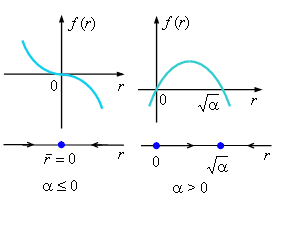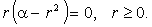(на примере реакционной схемы в реакторах идеального смешения и трубчатого)
1. Бифуркация Андронова-Хопфа
|
1.1. Описание бифуркации Андронова-Хопфа
Рассмотрим систему уравнений:
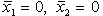 при любых значениях параметра при любых значениях параметра  .
Исследуем её на устойчивость при .
Исследуем её на устойчивость при  < 0, < 0,  > 0, > 0,  = 0. = 0.
Матрица А линеаризованной системы в точке 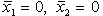 имеет вид: имеет вид:
 < 0 неподвижная точка < 0 неподвижная точка 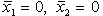 является устойчивым фокусом,
а при является устойчивым фокусом,
а при  > 0 - неустойчивым фокусом. При > 0 - неустойчивым фокусом. При  = 0 собственные числа располагаются на мнимой оси,
и об устойчивости состояния равновесия нельзя судить по линеаризованной системе. = 0 собственные числа располагаются на мнимой оси,
и об устойчивости состояния равновесия нельзя судить по линеаризованной системе.
Для исследования фазового портрета системы (12.1) удобно ввести полярные координаты, в которых система (12.1) примет вид:
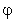 играет роль времени: играет роль времени: 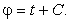 Следовательно, наиболее существенная информация о структуре траекторий содержится в первом уравнении системы (12.2).
Следовательно, наиболее существенная информация о структуре траекторий содержится в первом уравнении системы (12.2).
Определим неподвижные точки уравнения (12.2):
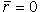 существует при любых значениях параметра существует при любых значениях параметра  :
при :
при 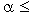 0 она является аттрактором, а при 0 она является аттрактором, а при  > 0 - репеллером.
При > 0 - репеллером.
При 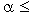 0 других неподвижных точек нет.
При 0 других неподвижных точек нет.
При  > 0 уравнение (12.2) имеет ещё одну неподвижную точку > 0 уравнение (12.2) имеет ещё одну неподвижную точку 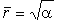 ,
которая является аттрактором (см. рисунок). ,
которая является аттрактором (см. рисунок).
Неподвижная точка 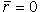 уравнения (12.2)
отвечает неподвижной точке уравнения (12.2)
отвечает неподвижной точке 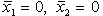 системы (12.1),
а неподвижная точка системы (12.1),
а неподвижная точка 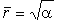 соответствует устойчивой замкнутой траектории - предельному циклу, представляющему собой окружность радиусом соответствует устойчивой замкнутой траектории - предельному циклу, представляющему собой окружность радиусом 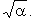
Таким образом, при переходе параметра  через нуль слева направо устойчивый фокус становится неустойчивым,
и от него отделяется предельный цикл - окружность, диаметр которой растёт пропорционально величине через нуль слева направо устойчивый фокус становится неустойчивым,
и от него отделяется предельный цикл - окружность, диаметр которой растёт пропорционально величине  .
Такое явление называется бифуркацией рождения цикла и в честь авторов, исследовавших этот тип бифуркации, - бифуркацией Андронова-Хопфа. .
Такое явление называется бифуркацией рождения цикла и в честь авторов, исследовавших этот тип бифуркации, - бифуркацией Андронова-Хопфа.
|