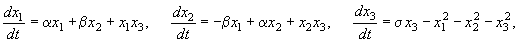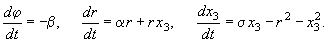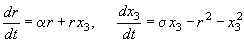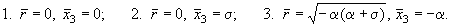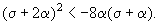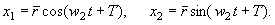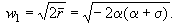(на примере реакционной схемы в реакторах идеального смешения и трубчатого)
4. Бифуркация рождения двумерного тора из предельного цикла в трёхмерном фазовом пространстве
|
4.2. Возникновение тора при бифуркации
Рассмотрим систему уравнений
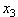 = 0)
на плоскости = 0)
на плоскости 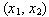 неподвижную точку - фокус. неподвижную точку - фокус.
Введение полярных координат на плоскости 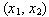 преобразует систему (12.10) к виду: преобразует систему (12.10) к виду:
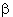 на плоскости на плоскости 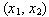 не зависит от того, каким образом переменная
не зависит от того, каким образом переменная 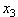 связана с связана с 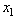 и и 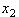 . .
Система
 < 0, < 0, 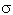 < 0,
неустойчива при < 0,
неустойчива при  > 0, > 0, 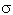 > 0
и является седлом при > 0
и является седлом при  < 0, < 0, 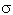 > 0
или > 0
или  > 0, > 0, 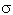 < 0. < 0.
Вторая точка устойчива при (  + + 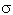 ) < 0, ) < 0,
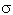 > 0, неустойчива при ( > 0, неустойчива при ( + + 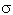 ) > 0, ) > 0,
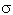 < 0 и является седлом при ( < 0 и является седлом при ( + + 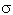 ) < 0, ) < 0,
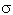 < 0. < 0.
Третья точка существует при  ( ( + + 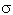 ) < 0
и является фокусом при выполнении условия: ) < 0
и является фокусом при выполнении условия:
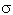 < -2 < -2 действительные части собственных чисел отрицательны и фокус устойчив.
Это означает, что на плоскости
действительные части собственных чисел отрицательны и фокус устойчив.
Это означает, что на плоскости 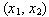 при
при 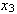 = - = -  существует устойчивое периодическое движение с частотой
существует устойчивое периодическое движение с частотой 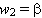 и радиусом
и радиусом 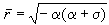 , т.е. предельный цикл: , т.е. предельный цикл:
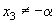 также притягиваются к этому предельному циклу. также притягиваются к этому предельному циклу.
При 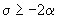 фокус теряет устойчивость, и в результате бифуркации Андронова-Хопфа на плоскости (r,
фокус теряет устойчивость, и в результате бифуркации Андронова-Хопфа на плоскости (r, 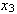 )
возникает предельный цикл с угловой частотой )
возникает предельный цикл с угловой частотой 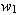 ,
в общем случае несоизмеримой с угловой частотой ,
в общем случае несоизмеримой с угловой частотой 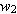 : :
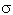 = -2 = -2  предельный цикл (12.11) на плоскости
предельный цикл (12.11) на плоскости 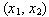 теряет устойчивость, и в трёхмерном пространстве возникает притягивающий двумерный тор с квазипериодическим
движением, если условия
теряет устойчивость, и в трёхмерном пространстве возникает притягивающий двумерный тор с квазипериодическим
движением, если условия  ( ( + + 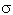 ) < 0
и ) < 0
и 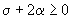 совместимы. совместимы.
Точка 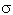 = -2 = -2  является точкой бифуркации рождения двумерного тора из предельного цикла в трёхмерном пространстве.
является точкой бифуркации рождения двумерного тора из предельного цикла в трёхмерном пространстве.
|