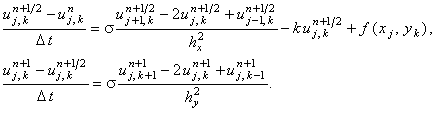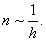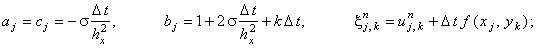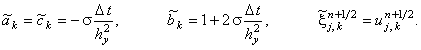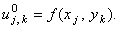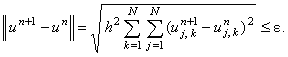4. Метод установления с использованием схемы расщепления.
|
Запишем для уравнения (11.2) схему расщепления:
Каждая из подсхем схемы расщепления (11.7) решается с помощью метода прогонки. Коэффициенты, соответствующие уравнению (4.10), имеют вид: для первой подсхемы
Легко видеть, что для обеих подсхем схемы расщепления (11.7) достаточное условие сходимости прогонки (4.16)
выполняется. Алгоритм решения схемы (11.7), а также методики определения прогоночных коэффициентов и
решения на правой границе аналогичны описанным ранее.
Также как и в случае метода простой итерации, в качестве нулевой итерации (начального условия, необходимого для решения в связи с введением фиктивной производной по времени) обычно задают свободный член:
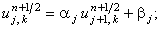 для второй подсхемы
для второй подсхемы 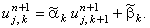
|