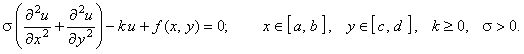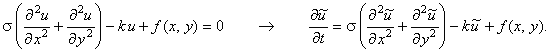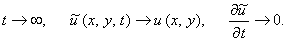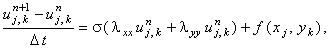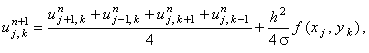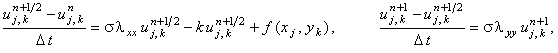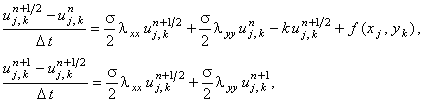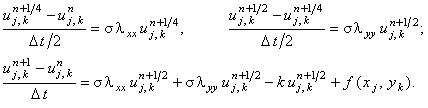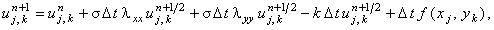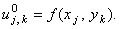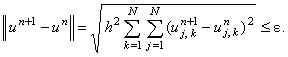7. Обобщение изученных методов.
|
В заключение приведём обобщение методов численного решения дифференциальных уравнений эллиптического типа:
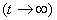 производная по времени будет стремиться к нулю, а решение нестационарной задачи -
к решению исходной стационарной задачи: производная по времени будет стремиться к нулю, а решение нестационарной задачи -
к решению исходной стационарной задачи:
Для осуществления итерационного процесса (т.е. для решения нестационарной задачи) используются следующие разностные схемы: 1. явная разностная схема (метод простой итерации; рассматривается для случая k = 0)
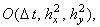 условно устойчива
условно устойчива 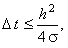 решается с помощью итерационного соотношения
решается с помощью итерационного соотношения
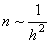 итераций; итераций;
2. схема расщепления
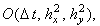 абсолютно устойчива,
каждая подсхема решается с помощью метода прогонки,
требует
абсолютно устойчива,
каждая подсхема решается с помощью метода прогонки,
требует 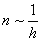 итераций; итераций;
3. схема переменных направлений
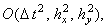 абсолютно устойчива,
каждая подсхема решается с помощью метода прогонки,
требует
абсолютно устойчива,
каждая подсхема решается с помощью метода прогонки,
требует 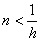 итераций; итераций;
4. схема предиктор-корректор
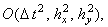 абсолютно устойчива,
абсолютно устойчива,
каждая из подсхем предиктора решается с помощью метода прогонки,
корректор - с помощью итерационного соотношения:
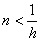 итераций. итераций.
При использовании любой из перечисленных разностных схем в качестве нулевой итерации (начального условия, необходимого для решения в связи с введением фиктивной производной по времени) задают свободный член:
Следует отметить, что метод установления требует соблюдения следующих правил при введении фиктивной производной по времени: 1) исходное стационарное уравнение предварительно должно быть приведено к виду (11.10), т.е. производные второго порядка должны находится в правой части уравнения и иметь положительный знак; 2) фиктивная производная по времени должна быть введена в левую часть уравнения и иметь положительный знак. |