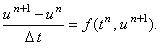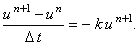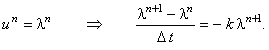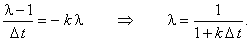2. Неявный метод Эйлера.
|
Запишем для уравнения (12.1) неявную разностную схему:
Также как и явная разностная схема (12.2), неявная разностная схема (12.4) имеет первый порядок аппроксимации по времени. Однако рекуррентное соотношение для её решения в общем виде не может быть получено (отметим, что оно вообще может быть получено не всегда). Для анализа устойчивости неявного метода Эйлера рассмотрим неявную разностную схему, аппроксимирующую уравнение (12.3):
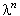 ,
и выражаем ,
и выражаем  : :
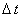 ; следовательно, неявная разностная схема,
аппроксимирующая уравнение (12.3), является абсолютно устойчивой. ; следовательно, неявная разностная схема,
аппроксимирующая уравнение (12.3), является абсолютно устойчивой.
Таким образом, неявный метод Эйлера является абсолютно устойчивым; однако он, также как и явный метод Эйлера, относится к методам с первым порядком точности. |