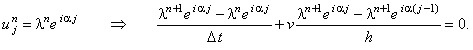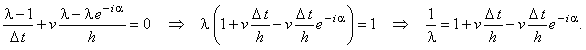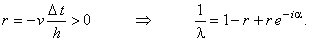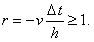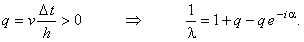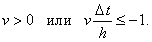|
6.1. Исследование устойчивости.
Исследуем устойчивость разностной схемы (5.5) с помощью спектрального метода.
Для этого отбрасываем член 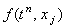 , наличие которого, как известно, не оказывает влияния на устойчивость
разностной схемы, и представляем решение в виде гармоники (3.7): , наличие которого, как известно, не оказывает влияния на устойчивость
разностной схемы, и представляем решение в виде гармоники (3.7):
Упрощаем данное выражение, деля левую и правую его части на 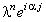 ,
и выражаем величину, обратную ,
и выражаем величину, обратную  :
Комплексный вид полученного выражения свидетельствует о том, что для устойчивости разностной схемы
(5.5) согласно условию (5.7) требуется, чтобы величины,
обратные собственным числам оператора перехода, были расположены вне или на
границе круга радиусом 1, центр которого находится в начале координат комплексной плоскости. :
Комплексный вид полученного выражения свидетельствует о том, что для устойчивости разностной схемы
(5.5) согласно условию (5.7) требуется, чтобы величины,
обратные собственным числам оператора перехода, были расположены вне или на
границе круга радиусом 1, центр которого находится в начале координат комплексной плоскости.
1. Рассмотрим случай v < 0. Введём следующее обозначение:
Полученное выражение свидетельствует о том, что величины, обратные собственным числам оператора
перехода, расположены на комплексной плоскости на окружности с центром в точке 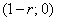 и радиусом r.
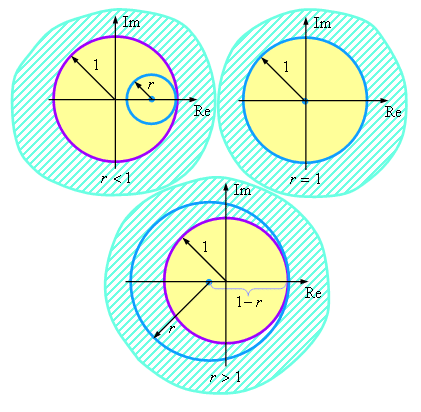
Сравнивая расположение этой окружности на комплексной плоскости с условием (5.7), получаем
три различных варианта (см. рисунок). Видно, что окружность, соответствующая величинам и радиусом r.
Сравнивая расположение этой окружности на комплексной плоскости с условием (5.7), получаем
три различных варианта (см. рисунок). Видно, что окружность, соответствующая величинам 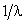 ,
при r < 1 находится внутри круга, соответствующего условию (5.7); при r > 1 - вне этого круга;
а при r = 1 совпадает с его границей. Таким образом, при отрицательном значении параметра v
неявная разностная схема (5.5) будет устойчива при выполнении следующего условия: ,
при r < 1 находится внутри круга, соответствующего условию (5.7); при r > 1 - вне этого круга;
а при r = 1 совпадает с его границей. Таким образом, при отрицательном значении параметра v
неявная разностная схема (5.5) будет устойчива при выполнении следующего условия:
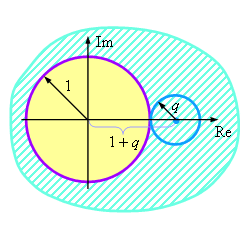
2. Рассмотрим случай v > 0. Введём следующее обозначение:
Полученное выражение свидетельствует о том, что величины, обратные собственным числам оператора
перехода, расположены на комплексной плоскости на окружности с центром в точке 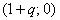 и радиусом q.
Данная окружность находится вне круга, соответствующего условию (5.7) при любом значении q (см. рисунок).
Таким образом, при положительном значении параметра v неявная разностная схема (5.5) будет устойчива. и радиусом q.
Данная окружность находится вне круга, соответствующего условию (5.7) при любом значении q (см. рисунок).
Таким образом, при положительном значении параметра v неявная разностная схема (5.5) будет устойчива.
Обобщая полученные результаты, сделаем вывод,
что неявная разностная схема с аппроксимацией производной по координате левой конечной разностью
(5.5) будет устойчива при выполнении одного из условий:
| |
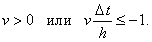 |
(5.10) |
Из соотношения (5.10) видно, что в частном случае при положительном значении параметра v рассматриваемая
разностная схема является абсолютно устойчивой.
|
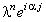 ,
и выражаем величину, обратную
,
и выражаем величину, обратную  :
:
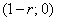 и радиусом r.
Сравнивая расположение этой окружности на комплексной плоскости с условием (5.7), получаем
три различных варианта (см. рисунок). Видно, что окружность, соответствующая величинам
и радиусом r.
Сравнивая расположение этой окружности на комплексной плоскости с условием (5.7), получаем
три различных варианта (см. рисунок). Видно, что окружность, соответствующая величинам 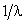 ,
при r < 1 находится внутри круга, соответствующего условию (5.7); при r > 1 - вне этого круга;
а при r = 1 совпадает с его границей. Таким образом, при отрицательном значении параметра v
неявная разностная схема (5.5) будет устойчива при выполнении следующего условия:
,
при r < 1 находится внутри круга, соответствующего условию (5.7); при r > 1 - вне этого круга;
а при r = 1 совпадает с его границей. Таким образом, при отрицательном значении параметра v
неявная разностная схема (5.5) будет устойчива при выполнении следующего условия:
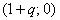 и радиусом q.
Данная окружность находится вне круга, соответствующего условию (5.7) при любом значении q (см. рисунок).
Таким образом, при положительном значении параметра v неявная разностная схема (5.5) будет устойчива.
и радиусом q.
Данная окружность находится вне круга, соответствующего условию (5.7) при любом значении q (см. рисунок).
Таким образом, при положительном значении параметра v неявная разностная схема (5.5) будет устойчива.
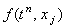 , наличие которого,
, наличие которого,