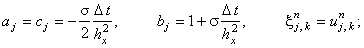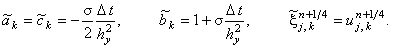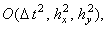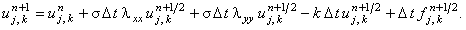Решение двумерных дифференциальных уравнений параболического типа.
       9. Схема предиктор-корректор.
     9.2. Характеристика подсхем.

     Каждая из подсхем, составляющих предиктор (7.15), (7.16), является абсолютно устойчивой и решается с помощью метода прогонки. Коэффициенты, соответствующие уравнению (4.10), имеют вид:

  • для первой подсхемы предиктора (7.15)
     
  • для второй подсхемы предиктора (7.16)
     
    Легко видеть, что для обеих подсхем достаточное условие сходимости прогонки (4.16) выполняется.

         Правая часть корректора (7.17) аппроксимируется относительно точки 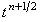. Это означает, что разностный оператор в левой части является центральной конечной разностью, которая, как известно, имеет второй порядок аппроксимации. Следовательно, роль корректора (7.17) в схеме предиктор-корректор (7.15)-(7.17) заключается в повышении порядка аппроксимации схемы по времени:
     
    что делает её более точной по сравнению со схемой расщепления (7.7), (7.8).
         Для решения корректора (7.17) используется рекуррентное соотношение, которое с учётом обозначений (7.6) имеет вид:
      (7.18)

         Итак, роль предиктора (7.15), (7.16) в схеме предиктор-корректор (7.15)-(7.17) заключается в обеспечении абсолютной устойчивости всей схемы; роль корректора (7.17) - в повышении порядка аппроксимации схемы по времени.