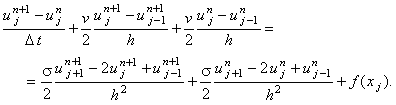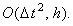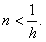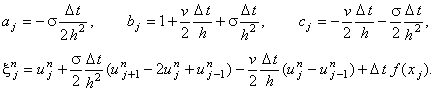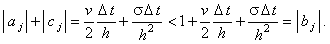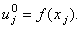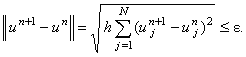Запишем для уравнения (10.4) разностную схему Кранка-Николсона (соблюдая правило выбора конечной разности для аппроксимации первой производной по координате):

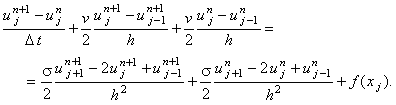(10.10)

Как и неявная разностная схема (10.9), разностная схема Кранка-Николсона (10.10) является абсолютно устойчивой, что обеспечивает возможность произвольного выбора значения шага итерации. Однако разностная схема Кранка-Николсона (10.10) имеет более высокий (второй) порядок аппроксимации по времени: Данная особенность разностной схемы Кранка-Николсона (10.10) позволяет использовать при её решении более грубый шаг итерации, чем при решении неявной разностной схемы (10.9), для получения результатов с такой же точностью; а это в свою очередь способствует ускорению сходимости итерационного процесса и уменьшению количества итераций:
     В разделе 6.4 было показано, что разностные схемы типа (10.10) решаются с помощью метода прогонки. Коэффициенты, соответствующие уравнению (4.10), для разностной схемы (10.10) имеют вид: Легко видеть, что достаточное условие сходимости прогонки (4.16) выполняется: Алгоритм решения, а также методики определения прогоночных коэффициентов и решения на правой границе аналогичны описанным ранее.
     Также как и в случае метода простой итерации, в качестве нулевой итерации (начального условия, необходимого для решения в связи с введением фиктивной производной по времени) обычно задают свободный член: Расчёт итераций продолжается до тех пор, пока итерационный процесс не сойдётся, т.е. пока не будет выполняться условие (10.5), в разностном представлении соответствующее неравенству: Итерационным выражением является прогоночное соотношение (4.11), имеющее такой же вид, как и в общем случае.